12 Латентно-семантический анализ

12.1 Векторы в лингвистике

Векторные представления слов - это совокупность подходов к моделированию языка, которые позволяют осуществлять семантический анализ слов и составленных из них документов. Например, находить синонимы и квазисинонимы, а также анализировать значения слов в диахронной перспективе.

В математике вектор – это объект, у которого есть длина и направление, заданные координатами вектора. Мы можем изобразить вектор в двумерном или трехмерном пространстве, где таких координат две или три (по числу измерений), но это не значит, что не может быть 100- или даже 1000-мерного вектора: математически это вполне возможно. Обычно, когда говорят о векторах слов, имеют в виду именно многомерное пространство.

Что в таком случае соответствует измерениям и координатам? Есть несколько возможных решений.

Мы можем, например, создать матрицу термин-документ, где каждое слово “описывается” вектором его встречаемости в различных документах (разделах, параграфах…). Слова считаются похожими, если “похожи” их векторы (о том, как сравнивать векторы, мы скажем чуть дальше). Аналогично можно сравнивать и сами документы.

Второй подход – зафиксировать совместную встречаемость (или другую меру ассоциации) между словами. В таком случае мы строим матрицу термин-термин. За контекст в таком случае часто принимается произвольное контекстное окно, а не целый документ. Небольшое контекстное окно (на уровне реплики) скорее сохранит больше синтаксической информации. Более широкое окно позволяет скорее судить о семантике: в таком случае мы скорее заинтересованы в словах, которые имеют похожих соседей.

И матрица термин-документ, и матрица термин-термин на реальных данных будут длинными и сильно разреженными (sparse), т.е. большая часть значений в них будет равна 0. С точки зрения вычислений это не представляет большой трудности, но может служить источником “шума”, поэтому в обработке естественного языка вместо них часто используют так называемые плотные (dense) векторы. Для этого к исходной матрице применяются различные методы снижения размерности.

В этом уроке мы рассмотрим алгоритм LSA и векторные модели на основе PMI. В первом случае анализируется матрица термин-документ, во втором – матрица термин-термин. Оба подхода предполагают использование SVD.

12.2 SVD

Для любых текстовых данных и матрица термин-термин и матрица термин-документ будет очень разряженной (то есть большая часть значений будет равна нулю). Необходимо “переупорядочить” ее так, чтобы сгруппировать слова и документы по темам и избавиться от малоинформативных тем.

Для этого используется алгебраическая процедура под названием сингулярное разложение матрицы (SVD). При сингулярном разложении исходная матрица \(A_r\) проецируется в пространство меньшей размерности, так что получается новая матрица \(A_k\), которая представляет собой малоранговую аппроксимацию исходной матрицы (К. Маннинг, П. Рагхаван, Х. Шютце 2020, 407).

Для получения новой матрицы применяется следующая процедура. Сначала для матрицы \(A_r\) строится ее сингулярное разложение (Singular Value Decomposition) по формуле: \(A = UΣV^t\) . Иными словами, одна матрица представляется в виде произведения трех других, из которых средняя - диагональная.

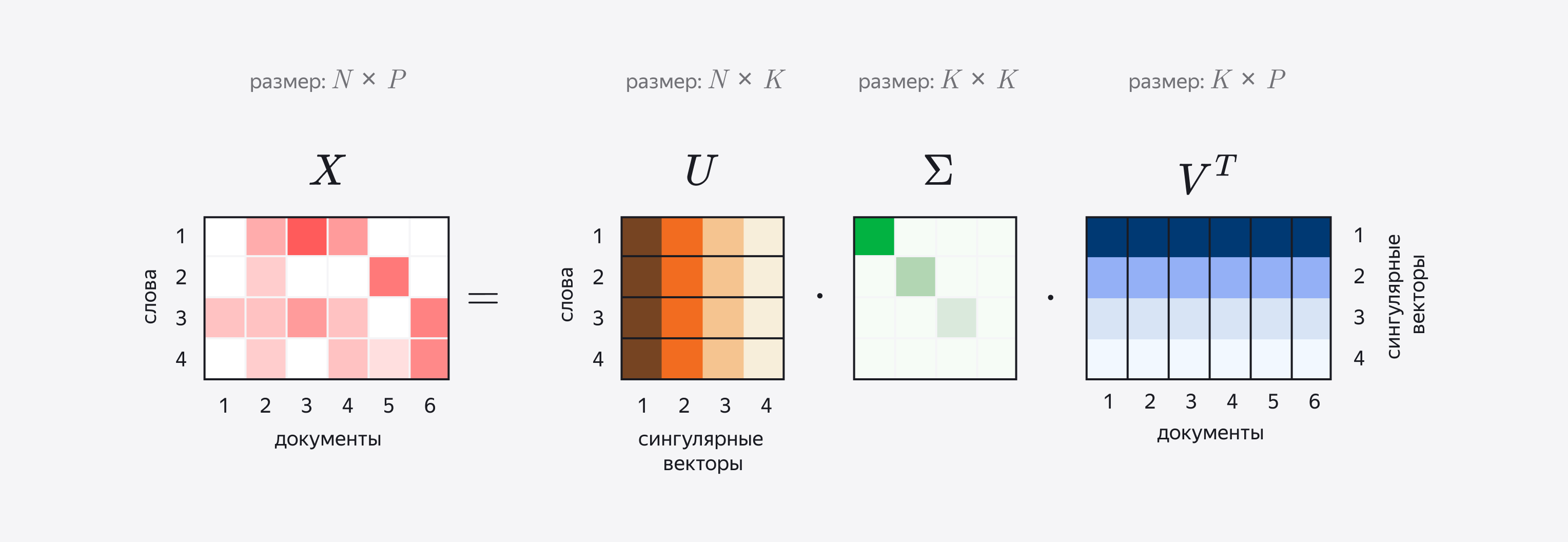
Здесь U — матрица левых сингулярных векторов матрицы A; Σ — диагональная матрица сингулярных чисел матрицы A; V — матрица правых сингулярных векторов матрицы A. О сингулярных векторах можно думать как о топиках-измерениях, которые задают пространство для наших документов.

Строки матрицы U соответствуют словам, при этом каждая строка состоит из элементов разных сингулярных векторов (на иллюстрации они показаны разными оттенками). Аналогично в V^t столбцы соответствуют отдельным документам. Следовательно, кажда строка матрицы U показывает, как связаны слова с топиками, а столбцы V^T – как связаны топики и документы.

Некоторые векторы соответствуют небольшим сингулярным значениям (они хранятся в диагональной матрице) и потому хранят мало информации, поэтому на следующем этапе их отсекают. Для этого наименьшие значения в диагональной матрице заменяются нулями. Такое SVD называется усеченным. Сколько топиков оставить при усечении, решает человек.

Собственно эмбеддингами, или векторными представлениями слова, называют произведения каждой из строк матрицы U на Σ, а эмбеддингами документа – произведение столбцов V^t на Σ. Таким образом мы как бы “вкладываем” (англ. embed) слова и документы в единое семантическое пространство, число измерений которого будет равно числу сингулярных векторов.

Посмотрим теперь, как SVD применяется при анализе текста.

12.3 Латентно-семантический анализ

LSA (Latent Semantic Analysis), или LSI (Latent Semantic Indexing) – это метод семантического анализа текста, который позволяет сопоставить слова и документы с некоторыми темами (топиками). Слово “latent” (англ. “скрытый”) в названии указывает на то, сами темы заранее не известны, и задача алгоритма как раз и заключается в том, чтобы их выявить.

Создатели метода LSA опираются на основополагающий принцип дистрибутивной семантики, согласно которому смысл слова определяется его контекстами, а смысл предложений и целых документов представляет собой своего рода сумму (или среднее) отдельных слов. Этот принцип является общим для всех векторных моделей.

На входе алгоритм LSA требует матрицу термин-документ. Она может хранить сведения о встречаемости слов в документах, хотя нередко используется уже рассмотренная мера tf-idf. Это связано с тем, что не все слова (даже после удаления стоп-слов) служат хорошими показателями темы: слово “дорожное”, например, служит лучшим показателем темы, чем слово “происшествие”, которое можно встретить и в других контекстах. Tf-idf понижает веса для слов, которые присутствуют во многих документах коллекции. Общий принцип действия алгоритма подробно объясняется на очень простом примере по ссылке; мы же перейдем сразу к анализу реальных данных.

12.4 Подгтовка данных

Мы воспользуемся датасетом с подборкой новостей на русском языке (для простоты возьмем из него лишь один год). Файл в формате .Rdata можно скачать в формате .Rdata по ссылке.

library(tidyverse)
load("../data/news.Rdata")

news_2019 |> 
  mutate(text = str_trunc(text, 70))

Добавим id для документов.

news_2019 <- news_2019 |> 
  mutate(id = paste0("doc", row_number()))

Составим список стоп-слов.

library(stopwords)
stopwords_ru <- c(
  stopwords("ru", source = "snowball"),
  stopwords("ru", source = "marimo"),
  stopwords("ru", source = "nltk"), 
  stopwords("ru", source  = "stopwords-iso")
  )

stopwords_ru <- sort(unique(stopwords_ru))
length(stopwords_ru)

[1] 715

Разделим статьи на слова и удалим стоп-слова; это может занять несколько минут.

library(tidytext)
news_tokens <- news_2019 |> 
  unnest_tokens(token, text) |> 
  filter(!token %in% stopwords_ru)

Многие слова встречаются всего несколько раз и для тематического моделирования бесполезны. Поэтому можно от них избавиться.

news_tokens_pruned <- news_tokens |> 
  add_count(token) |> 
  filter(n > 10) |> 
  select(-n)

Также избавимся от цифр, хотя стоит иметь в виду, что их пристутствие в тексте может быть индикатором темы: в некоторых случах лучше не удалять цифры, а, например, заменять их на некую последовательность символов вроде digit и т.п. Токены на латинице тоже удаляем.

news_tokens_pruned <- news_tokens_pruned |> 
  filter(str_detect(token, "[\u0400-\u04FF]")) |> 
  filter(!str_detect(token, "\\d"))

Warning in rm(news_tokens): object 'news_tokens' not found

news_tokens_pruned

Посмотрим на статистику по словам.

news_tokens_pruned |> 
  group_by(token) |> 
  summarise(n = n()) |> 
  arrange(-n)

Этап подготовки данных – самый трудоемкий и не самый творческий, но не стоит им пренебрегать, потому что от этой работы напрямую зависит качество модели.

12.5 TF-IDF: опрятный подход

Вместо показателей абсолютной встречаемости при анализе больших текстовых данных применяется tf-idf. Эта статистическая мера не используется, если дана матрица термин-термин, но она хорошо работает с матрицами термин-документ, позволяя повысить веса для тех слов, которые служат хорошими дискриминаторами. Например, “заявил” и “отметил”, хотя это не стоп-слова, могут встречаться в разных темах.

news_counts <- news_tokens_pruned |>
  count(token, id)

news_counts

news_counts |> 
  arrange(id)

Добавляем tf_idf.

news_tf_idf <- news_counts |> 
  bind_tf_idf(token, id, n) |> 
  arrange(tf_idf) |> 
  select(-n, -tf, -idf)

news_tf_idf

12.6 DocumentTermMatrix

Посмотрим на размер получившейся таблицы.

object.size(news_tf_idf)

5369712 bytes

format(object.size(news_tf_idf), units = "auto")

[1] "5.1 Mb"

Чтобы вычислить SVD, такую таблицу необходимо преобразовать в матрицу термин-документ. Оценим ее размер:

# число уникальных токенов
m <- unique(news_tf_idf$token) |> 
  length()
m

[1] 6299

# число уникальных документов
n <- unique(news_tf_idf$id) |> 
  length()  
n

[1] 3407

# число элементов в матрице 
m * n

[1] 21460693

Используем специальный формат для хранения разреженных матриц.

dtm <- news_tf_idf |> 
  cast_sparse(token, id, tf_idf)

# первые 10 рядов и 5 столбцов
dtm[1:10, 1:5]

10 x 5 sparse Matrix of class "dgCMatrix"
               doc608     doc1670     doc2170     doc2184     doc2219
ранее     0.003530193 .           .           0.005002585 .          
россии    0.010127611 0.003675658 0.004689633 0.004783897 0.005471238
словам    .           .           0.011776384 .           0.006869557
рублей    0.006686328 .           0.027865190 .           .          
рассказал 0.007250151 .           .           0.010274083 .          
данным    0.007406320 .           .           .           0.012003345
издание   0.007759457 .           .           .           0.012575671
ходе      0.008675929 .           .           .           .          
заявил    0.016729327 .           .           .           .          
частности 0.008860985 .           0.012309349 .           .

Снова уточним размер матрицы.

format(object.size(dtm), units = "auto")

[1] "3 Mb"

12.7 SVD с пакетом `irlba`

Метод для эффективного вычисления усеченного SVD на больших матрицах реализован в пакете irlba. Возможно, придется подождать ⏳.

library(irlba)
lsa_space<- irlba::irlba(dtm, 50)

Функция вернет список из трех элементов:

d: k аппроксимированных сингулярных значений;
u: k аппроксимированных левых сингулярных векторов;
v: k аппроксимированных правых сингулярных векторов.

Полученную LSA-модель можно использовать для поиска наиболее близких слов и документов или для изучения тематики корпуса – в последнем случае нас может интересовать, какие топики доминируют в тех или иных документах и какими словами они в первую очередь представлены.

12.8 Эмбеддинги слов

Вернем имена рядов матрице левых сингулярных векторов и добавим имена столбцов.

rownames(lsa_space$u) <- rownames(dtm)
colnames(lsa_space$u) <- paste0("dim", 1:50)

Теперь посмотрим на эмбеддинги слов.

word_emb <- lsa_space$u |> 
  as.data.frame() |> 
  rownames_to_column("word") |> 
  as_tibble()

word_emb

Преобразуем наши данные в длинный формат.

word_emb_long <- word_emb |> 
  pivot_longer(-word, names_to = "dimension", values_to = "value") |>
  mutate(dimension = as.numeric(str_remove(dimension, "dim")))
  

word_emb_long

12.9 Визуализация топиков

Визуализируем несколько топиков, чтобы понять, насколько они осмыслены.

word_emb_long |> 
  filter(dimension < 10) |> 
  group_by(dimension) |> 
  top_n(10, abs(value)) |> 
  ungroup() |> 
  mutate(word = reorder_within(word, value, dimension)) |> 
  ggplot(aes(word, value, fill = dimension)) +
  geom_col(alpha = 0.8, show.legend = FALSE) +
  facet_wrap(~dimension, scales = "free_y", ncol = 3) +
  scale_x_reordered() +
  coord_flip() +
  labs(
    x = NULL, 
    y = "Value",
    title = "Первые 9 главных компонент за 2019 г.",
    subtitle = "Топ-10 слов"
  ) +
  scale_fill_viridis_c()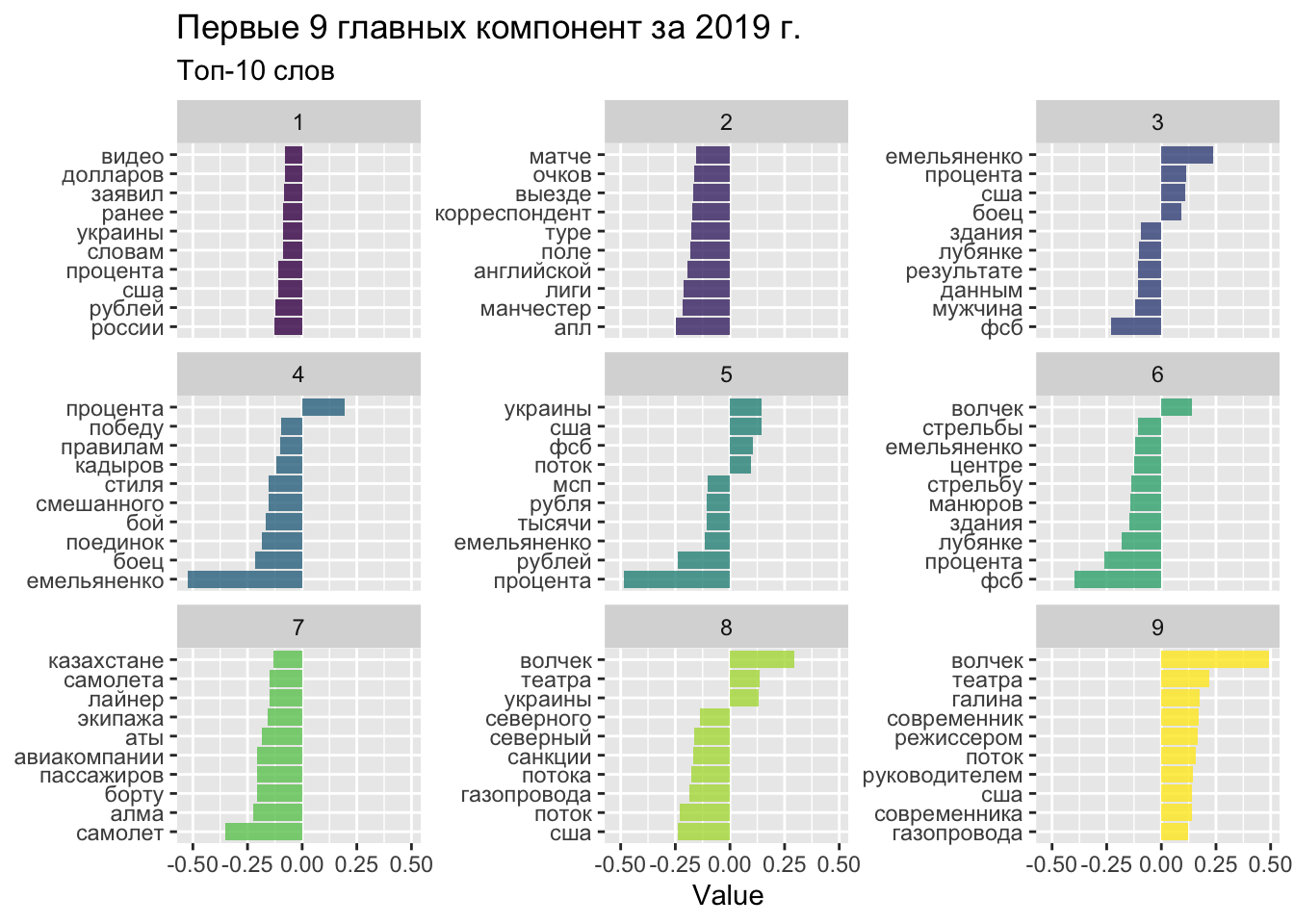

12.10 Ближайшие соседи

Эмбеддинги можно использовать для поиска ближайших соседей.

library(widyr)

nearest_neighbors <- function(df, feat, doc=F) {
  inner_f <- function() {
    widely(
        ~ {
          y <- .[rep(feat, nrow(.)), ]
          res <- rowSums(. * y) / 
            (sqrt(rowSums(. ^ 2)) * sqrt(sum(.[feat, ] ^ 2)))
          
          matrix(res, ncol = 1, dimnames = list(x = names(res)))
        },
        sort = TRUE
    )}
  if (doc) {
    df |> inner_f()(doc, dimension, value) }
  else {
    df |> inner_f()(word, dimension, value)
  } |> 
    select(-item2)
}

nearest_neighbors(word_emb_long, "сборная")

nearest_neighbors(word_emb_long, "завод")

12.11 Похожие документы

Информация о документах хранится в матрице правых сингулярных векторов.

rownames(lsa_space$v) <- colnames(dtm)
colnames(lsa_space$v) <- paste0("dim", 1:50)

Посмотрим на эмбеддинги документов.

doc_emb <- lsa_space$v |> 
  as.data.frame() |> 
  rownames_to_column("doc") |> 
  as_tibble()

doc_emb

Преобразуем в длинный формат.

doc_emb_long <- doc_emb |> 
  pivot_longer(-doc, names_to = "dimension", values_to = "value") |>
  mutate(dimension = as.numeric(str_remove(dimension, "dim")))
  

doc_emb_long

И найдем соседей для произвольного документа.

nearest_neighbors(doc_emb_long, "doc14", doc = TRUE)

Выведем документ 14 вместе с его соседями.

news_2019 |> 
  filter(id %in% c("doc14", "doc392", "doc2043")) |> 
  mutate(text = str_trunc(text, 70))

Поздравляем, вы построили свою первую рекомендательную систему ☕.

12.12 2D-визуализация пространства документов

Для снижения размерности мы используем алгоритм UMAP. В отличие от PCA, он снижает размерность нелинейно, и в этом отношении похож на t-SNE.

library(uwot)
set.seed(07062024)
viz_lsa <- umap(lsa_space$v ,  n_neighbors = 15, n_threads = 2)

Как видно по размерности матрицы, все документы вложены теперь в двумерное пространство.

dim(viz_lsa)

[1] 3407    2

Закодировав цветом рубрики новостного сайта, нанесем документы на “карту”.

tibble(doc = rownames(viz_lsa),
       topic = news_2019$topic,
       V1 = viz_lsa[, 1], 
       V2 = viz_lsa[, 2]) |> 
  ggplot(aes(x = V1, y = V2, label = doc, color = topic)) + 
  geom_text(size = 2, alpha = 0.8, position = position_jitter(width = 1.5, height = 1.5)) +
  annotate(geom = "rect", ymin = -10, ymax = 0, xmin = -20, xmax = -10, alpha = 0.2, color = "tomato") +
  theme_light()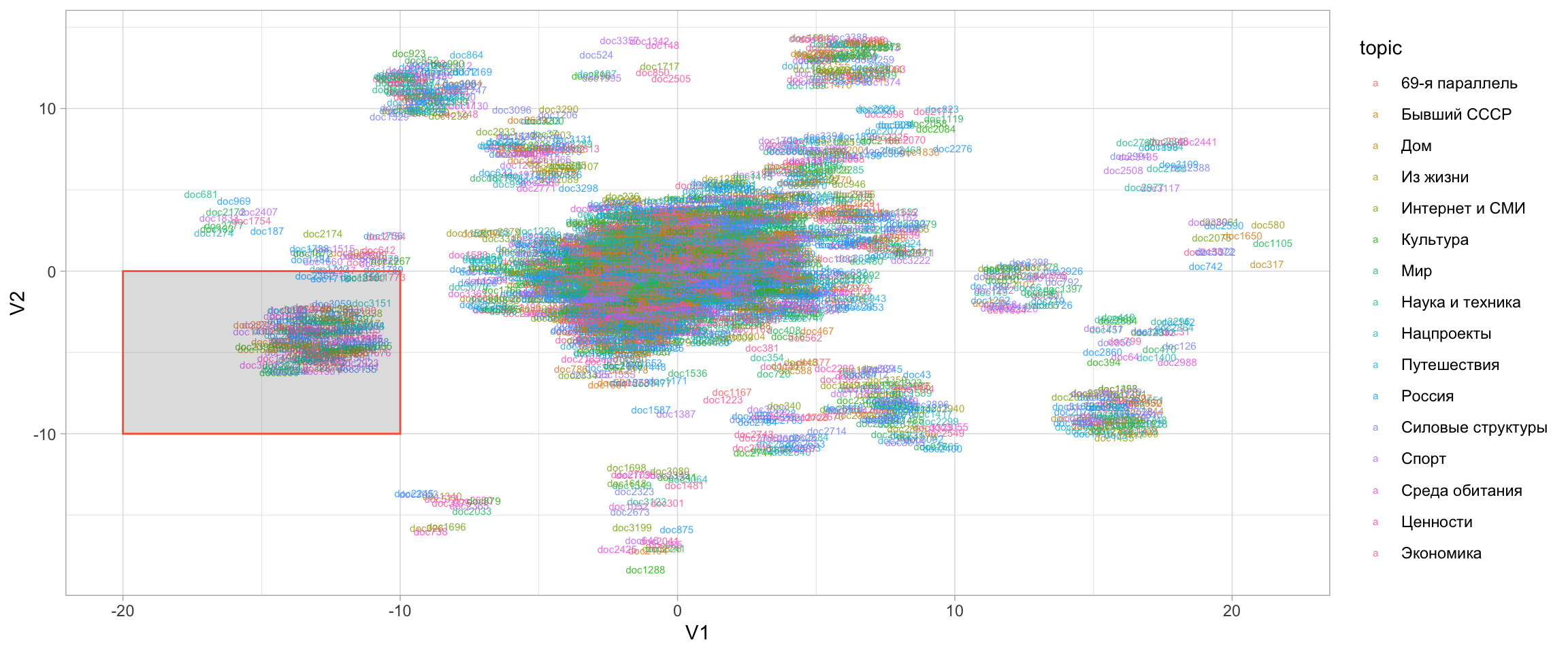

Вот несколько новостей из небольшого тематического кластера, выделенного на карте квадратом.

news_2019 |> 
  filter(id %in% c("doc718", "doc2437", "doc2918")) |> 
  mutate(text = str_trunc(text, 70))