library(tidyverse)
library(tidytext)
library(stopwords)
library(widyr)
library(uwot)
library(text)12 Векторные представления слов
12.1 Векторы в лингвистике
Векторные представления слов - это совокупность подходов к моделированию языка, которые позволяют осуществлять семантический анализ слов и составленных из них документов. Например, находить синонимы и квазисинонимы, а также анализировать значения слов в диахронной перспективе.
В математике вектор – это объект, у которого есть длина и направление, заданные координатами вектора. Мы можем изобразить вектор в двумерном или трехмерном пространстве, где таких координат две или три (по числу измерений), но это не значит, что не может быть 100- или даже 1000-мерного вектора: математически это вполне возможно. Обычно, когда говорят о векторах слов, имеют в виду именно многомерное пространство.
Что в таком случае соответствует измерениям и координатам? Есть несколько возможных решений.
Мы можем, например, создать матрицу термин-документ, где каждое слово “описывается” вектором его встречаемости в различных документах (разделах, параграфах…). Слова считаются похожими, если “похожи” их векторы (о том, как сравнивать векторы, мы скажем чуть дальше). Аналогично можно сравнивать и сами документы.
Второй подход – зафиксировать совместную встречаемость (или другую меру ассоциации) между словами. В таком случае мы строим матрицу термин-термин. За контекст в таком случае часто принимается произвольное контекстное окно, а не целый документ. Небольшое контекстное окно (на уровне реплики) скорее сохранит больше синтаксической информации. Более широкое окно позволяет скорее судить о семантике: в таком случае мы скорее заинтересованы в словах, которые имеют похожих соседей.
И матрица термин-документ, и матрица термин-термин на реальных данных будут длинными и сильно разреженными (sparse), т.е. большая часть значений в них будет равна 0. С точки зрения вычислений это не представляет большой трудности, но может служить источником “шума”, поэтому в обработке естественного языка вместо них часто используют так называемые плотные (dense) векторы, или эмбеддинги. Для этого к исходной матрице применяются различные методы снижения размерности.
Подробнее о векторных моделях можено почитать статью В. Селеверстова на “Системном блоке”, а также посмотреть видео с лекцией Д. Рыжовой.
В этом уроке мы изучим несколько способов пострения эмбеддингов:
- на основе совместной встречаемости слов с использованием PMI;
- с использованием поверхностной нейросети Word2Vec;
- c использованием трансформера BERT.
Также мы поговорим об использовании готовых (предобученных) эмбеддингов для разных языков.
12.2 Подготовка данных
Мы воспользуемся датасетом с подборкой новостей на русском языке (для ускорения вычислений возьмем из него лишь один год). Файл в формате .Rdata в формате .Rdata доступен по ссылке.
Код для приведения датасета к опрятному виду.
load("../data/news.Rdata")
news_2019 <- news_2019 |>
mutate(id = paste0("doc", row_number()))Составим список стоп-слов.
stopwords_ru <- c(
stopwords("ru", source = "snowball"),
stopwords("ru", source = "marimo"),
stopwords("ru", source = "nltk"),
stopwords("ru", source = "stopwords-iso")
)
stopwords_ru <- sort(unique(stopwords_ru))
length(stopwords_ru)Разделим статьи на слова и удалим стоп-слова; это может занять несколько минут.
news_tokens <- news_2019 |>
unnest_tokens(token, text) |>
filter(!token %in% stopwords_ru)Многие слова встречаются всего несколько раз и для тематического моделирования бесполезны. Поэтому можно от них избавиться.
news_tokens_pruned <- news_tokens |>
add_count(token) |>
filter(n > 10) |>
select(-n)Также избавимся от цифр, хотя стоит иметь в виду, что их пристутствие в тексте может быть индикатором темы: в некоторых случах лучше не удалять цифры, а, например, заменять их на некую последовательность символов вроде digit и т.п. Токены на латинице тоже удаляем.
news_tokens_pruned <- news_tokens_pruned |>
filter(str_detect(token, "[\u0400-\u04FF]")) |>
filter(!str_detect(token, "\\d"))news_tokens_prunedЭтап подготовки данных – самый трудоемкий и не самый творческий, но не стоит им пренебрегать, потому что от этой работы напрямую зависит качество модели.
Подготовленные данные можно забрать по ссылке.
load("../data/news_tokens_pruned.Rdata")12.3 PMI-SVD эмбеддинги
12.3.1 Скользящее окно
Прежде всего разделим новости на контекстные окна фиксированной величины. Чем меньше окно, тем больше синтаксической информации оно хранит.
nested_news <- news_tokens_pruned |>
dplyr::select(-topic) |>
nest(tokens = c(token))
nested_newsslide_windows <- function(tbl, window_size) {
skipgrams <- slider::slide(
tbl,
~.x,
.after = window_size - 1,
.step = 1,
.complete = TRUE
)
safe_mutate <- safely(mutate)
out <- map2(skipgrams,
1:length(skipgrams),
~ safe_mutate(.x, window_id = .y))
out |>
transpose() |>
pluck("result") |>
compact() |>
bind_rows()
}Деление на окна может потребовать нескольких минут. Чем больше окно, тем больше потребуется времени и тем больше будет размер таблицы.
news_windows <- nested_news |>
mutate(tokens = map(tokens, slide_windows, 8L)) |>
unnest(tokens) |>
unite(window_id, id, window_id)
news_windowsload("../data/news_windows.Rdata")12.3.2 Что такое PMI
Обычная мера ассоциации между словами, которой пользуются лингвисты, — точечная взаимная информация, или PMI (pointwise mutual information). Она рассчитывается по формуле:
\[PMI\left(x;y\right)=\log{\frac{P\left(x,y\right)}{P\left(x\right)P\left(y\right)}}\]
В числителе — вероятность встретить два слова вместе (например, в пределах одного документа или одного «окна» длинной n слов). В знаменателе — произведение вероятностей встретить каждое из слов отдельно. Если слова чаще встречаются вместе, логарифм будет положительным; если по отдельности — отрицательным.
Посчитаем PMI на наших данных, воспользовавшись подходящей функцией из пакета {widyr}.
news_pmi <- news_windows |>
pairwise_pmi(token, window_id)
news_pmi |>
arrange(-abs(pmi))12.3.3 Почему PPMI
В отличие от коэффициента корреляции, PMI может варьироваться от \(-\infty\) до \(+\infty\), но негативные значения проблематичны. Они означают, что вероятность встретить эти два слова вместе меньше, чем мы бы ожидали в результате случайного совпадения. Проверить это без огромного корпуса невозможно: если у нас есть \(w_1\) и \(w_2\), каждое из которых встречается с вероятностью \(10^{-6}\), то трудно удостовериться в том, что \(p(w_1, w_2)\) значимо отличается от \(10^{-12}\). Поэтому негативные значения PMI принято заменять нулями. В таком случае формула выглядит так:
\[ PMI\left(x;y\right)=max(\log{\frac{P\left(x,y\right)}{P\left(x\right)P\left(y\right)}},0) \] Для подобной замены подойдет векторизованное условие.
news_ppmi <- news_pmi |>
mutate(ppmi = case_when(pmi < 0 ~ 0,
.default = pmi))
news_ppmi |>
arrange(pmi)12.3.4 SVD
Для любых текстовых данных и матрица термин-термин будет очень разряженной (то есть большая часть значений будет равна нулю). Необходимо “переупорядочить” ее так, чтобы сгруппировать слова и документы по темам и избавиться от малоинформативных тем.
Для этого используется алгебраическая процедура под названием сингулярное разложение матрицы (SVD). При сингулярном разложении исходная матрица \(A_r\) проецируется в пространство меньшей размерности, так что получается новая матрица \(A_k\), которая представляет собой малоранговую аппроксимацию исходной матрицы (К. Маннинг, П. Рагхаван, Х. Шютце 2020, 407).
Для получения новой матрицы применяется следующая процедура. Сначала для матрицы \(A_r\) строится ее сингулярное разложение (Singular Value Decomposition) по формуле: \(A = UΣV^t\) . Иными словами, одна матрица представляется в виде произведения трех других, из которых средняя - диагональная.
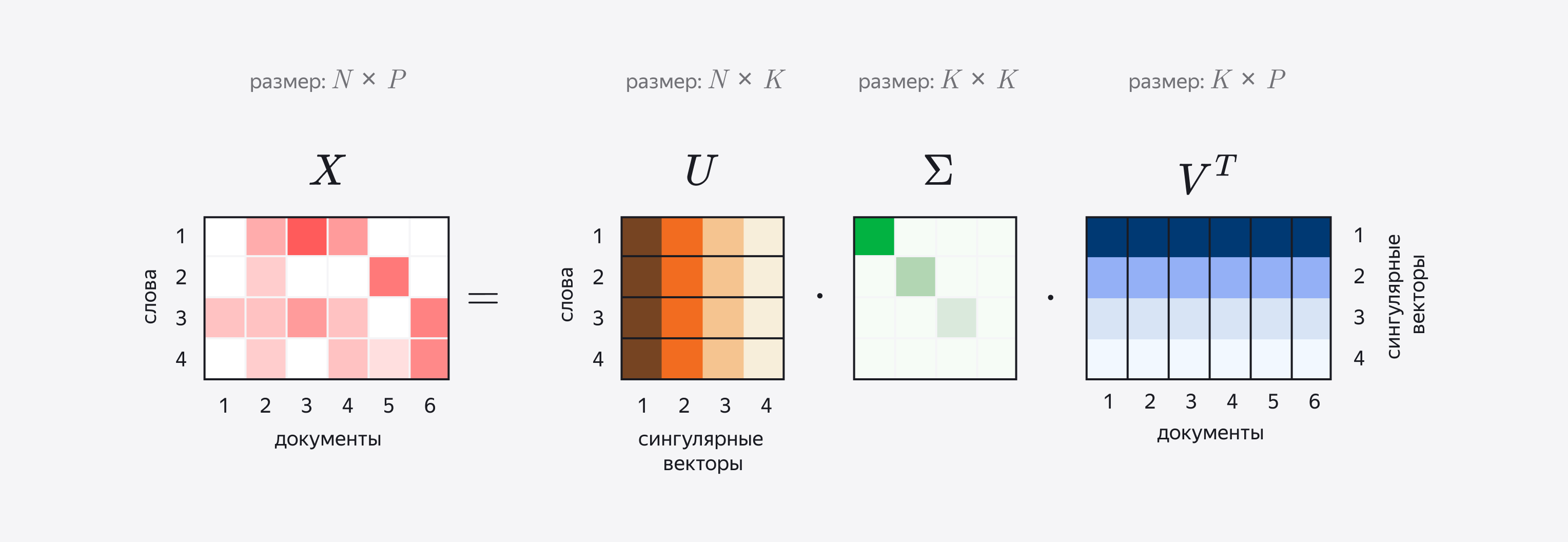
Здесь U — матрица левых сингулярных векторов матрицы A; Σ — диагональная матрица сингулярных чисел матрицы A; V — матрица правых сингулярных векторов матрицы A. О сингулярных векторах можно думать как о топиках-измерениях, которые задают пространство для наших документов.
Строки матрицы U соответствуют словам, при этом каждая строка состоит из элементов разных сингулярных векторов (на иллюстрации они показаны разными оттенками). Аналогично в V^t столбцы соответствуют отдельным документам. Следовательно, кажда строка матрицы U показывает, как связаны слова с топиками, а столбцы V^T – как связаны топики и документы.
Некоторые векторы соответствуют небольшим сингулярным значениям (они хранятся в диагональной матрице) и потому хранят мало информации, поэтому на следующем этапе их отсекают. Для этого наименьшие значения в диагональной матрице заменяются нулями. Такое SVD называется усеченным. Сколько топиков оставить при усечении, решает человек.
Собственно эмбеддингами, или векторными представлениями слова, называют произведения каждой из строк матрицы U на Σ, а эмбеддингами документа – произведение столбцов V^t на Σ. Таким образом мы как бы “вкладываем” (англ. embed) слова и документы в единое семантическое пространство, число измерений которого будет равно числу сингулярных векторов.
Передадим подготовленные данные фунции widely_svd() для вычисления сингулярного разложения. Число измерений для усеченного SVD задается вручную. Обратите внимание на аргумент weight_d: если задать ему значение FALSE, то вернутся не эмбеддинги, а матрица левых сингулярных векторов:
word_emb <- news_ppmi |>
widely_svd(item1, item2, ppmi,
weight_d = FALSE, nv = 100) |>
rename(word = item1) # иначе nearest_neighbors() будет жаловатьсяword_emb12.3.5 Визуализация топиков
Визуализируем главные компоненты нашего векторного пространства.
word_emb |>
filter(dimension < 10) |>
group_by(dimension) |>
top_n(10, abs(value)) |>
ungroup() |>
mutate(word = reorder_within(word, value, dimension)) |>
ggplot(aes(word, value, fill = dimension)) +
geom_col(alpha = 0.8, show.legend = FALSE) +
facet_wrap(~dimension, scales = "free_y", ncol = 3) +
scale_x_reordered() +
coord_flip() +
labs(
x = NULL,
y = "Value",
title = "Первые 9 главных компонент за 2019 г.",
subtitle = "Топ-10 слов"
) +
scale_fill_viridis_c()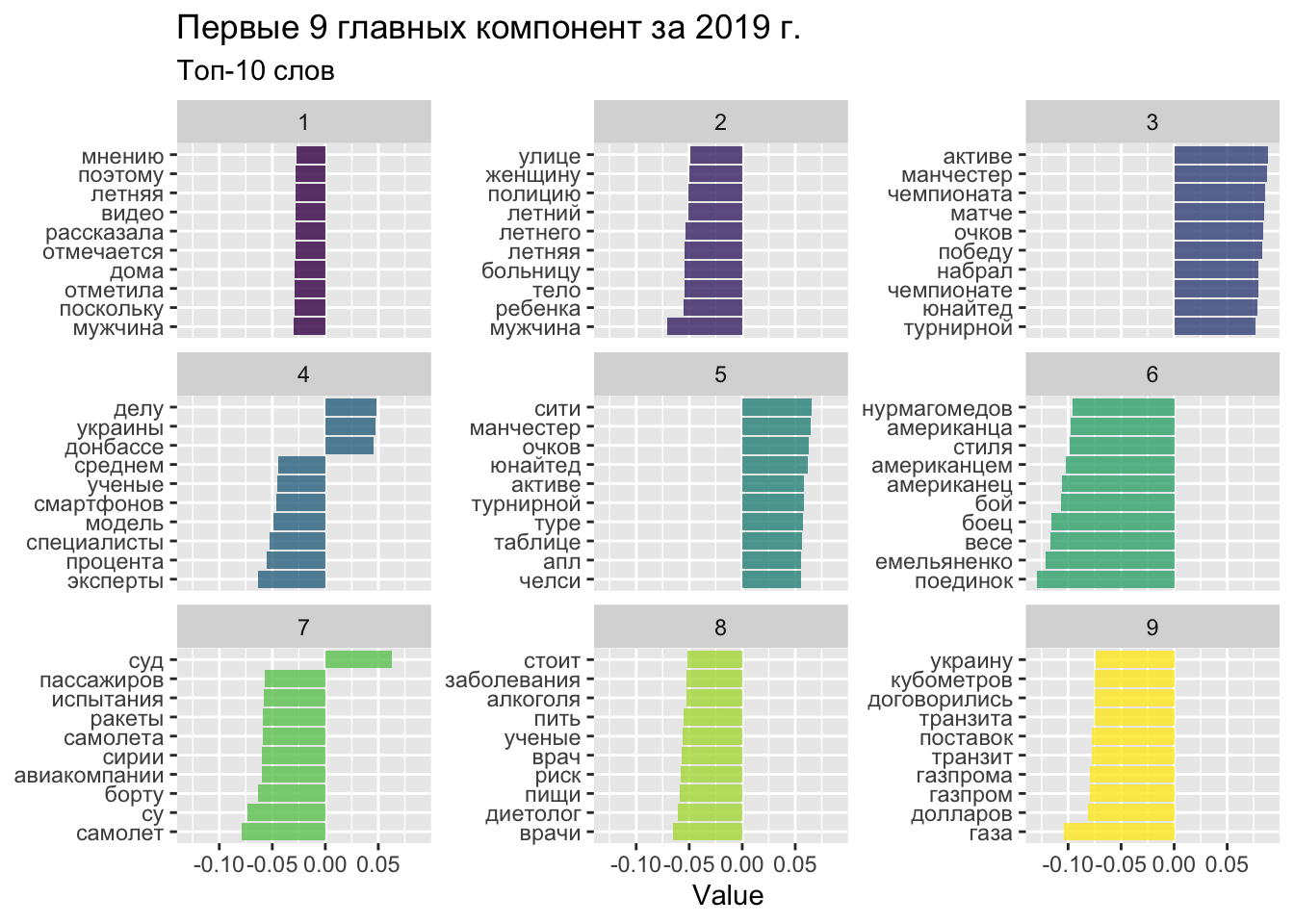
12.3.6 Ближайшие соседи
Исследуем наши эмбеддинги, используя функцию, которая считает косинусное сходство между словами.
nearest_neighbors <- function(df, feat, doc=F) {
inner_f <- function() {
widely(
~ {
y <- .[rep(feat, nrow(.)), ]
res <- rowSums(. * y) /
(sqrt(rowSums(. ^ 2)) * sqrt(sum(.[feat, ] ^ 2)))
matrix(res, ncol = 1, dimnames = list(x = names(res)))
},
sort = TRUE
)}
if (doc) {
df |> inner_f()(doc, dimension, value) }
else {
df |> inner_f()(word, dimension, value)
} |>
select(-item2)
}word_emb |>
nearest_neighbors("сборная")word_emb |>
nearest_neighbors("завод")12.3.7 2D-визуализации пространства слов
word_emb_mx <- word_emb |>
cast_sparse(word, dimension, value) |>
as.matrix()Для снижения размерности мы используем алгоритм UMAP. Это алгоритм нелинейного снижения размерности.
set.seed(02062024)
viz <- umap(word_emb_mx, n_neighbors = 15, n_threads = 2)Как видно по размерности матрицы, все слова вложены теперь в двумерное пространство.
dim(viz)[1] 6299 2tibble(word = rownames(word_emb_mx),
V1 = viz[, 1],
V2 = viz[, 2]) |>
ggplot(aes(x = V1, y = V2, label = word)) +
geom_text(size = 2, alpha = 0.4, position = position_jitter(width = 0.5, height = 0.5)) +
annotate(geom = "rect", ymin = 5, ymax = 8, xmin = -1, xmax = 2, alpha = 0.2, color = "tomato")+
theme_light()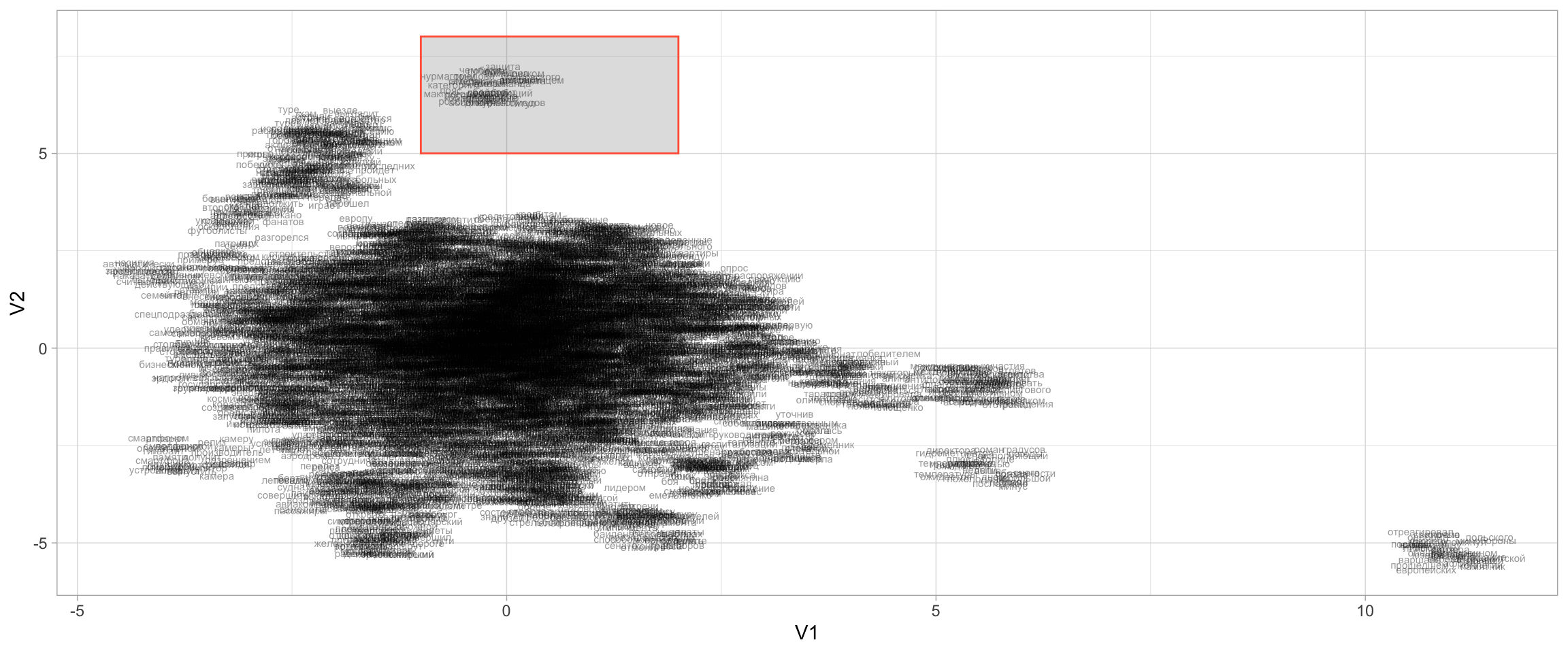
Посмотрим на выделенный фрагмент этой карты.
tibble(word = rownames(word_emb_mx),
V1 = viz[, 1],
V2 = viz[, 2]) |>
filter(V1 > -1 & V1 < 2) |>
filter(V2 > 5 & V2 < 8) |>
ggplot(aes(x = V1, y = V2, label = word)) +
geom_text(size = 5, alpha = 0.5,
position = position_jitter(width = 0.5, height = 0.5)
) +
theme_light()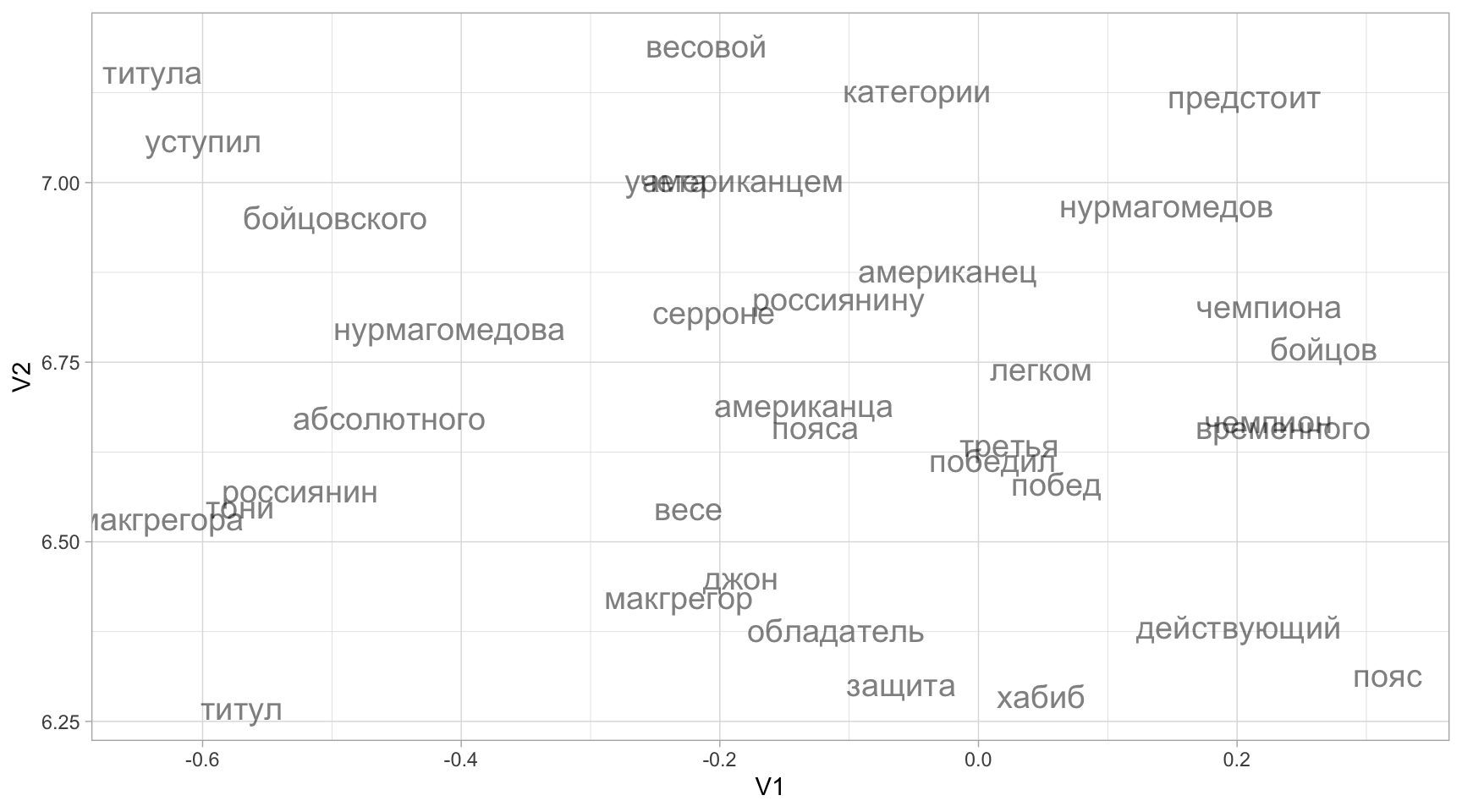
Отличная работа 🥊 Теперь попробуем построить векторное пространство с использованием поверхностных нейросетей.
12.4 Word2vec
Word2vec – это полносвязаная нейросеть с одним скрытым слоем. Такое обучение называется не глубоким, а поверхностным (shallow).
library(word2vec)
corpus_w2v <- news_tokens_pruned |>
group_by(id) |>
mutate(text = str_c(token, collapse = " ")) |>
distinct(id, text)# устанавливаем зерно, т.к. начальные веса устанавливаются произвольно
set.seed(02062024)
model <- word2vec(x = corpus_w2v$text,
type = "skip-gram",
dim = 100,
window = 10,
iter = 20,
hs = TRUE,
min_count = 5,
threads = 6)Наша модель содержит эмбеддинги для слов; посмотрим на матрицу.
emb <- as.matrix(model)
dim(emb)[1] 6305 100predict(model, c("погода", "спорт"), type = "nearest", top_n = 10) |>
bind_rows()Получившуюся модель можно визуализировать, как мы это делали выше.
12.5 BERT
BERT (Bidirectional Encoder Representations from Transformers) — это глубокая нейронная модель для обработки естественного языка, представленная Google в 2018 году. Главная особенность BERT — двунаправленное (bidirectional) чтение текста, позволяющее учитывать контекст слова как слева, так и справа. BERT обучается на задаче восстановления пропущенных слов в предложении и на предсказании, идут ли два предложения подряд.
Варианты BERT:
- BERT-base (12 слоев), BERT-large (24 слоя) — оригинальные модели разного размера.
- DistilBERT (6 слоев) — облегчённая и быстрая версия.
- RoBERTa, ALBERT, TinyBERT и др. — различные модификации BERT, оптимизированные для конкретных задач.
- Multilingual BERT (mBERT) — для многих языков сразу.
BERT генерирует контекстные эмбеддинги — числовые векторы, которые учитывают значение слова в конкретном контексте предложения. Благодаря этому BERT-эмбеддинги позволяют машинам лучше понимать смысл текста и эффективно применять их для поиска, классификации, вопросов-ответов и других NLP-задач.
Для большинства задач на русском языке (эмбеддинги, классификация, поиск) лучше использовать одну из RuBERT (или RuRoBERT) моделей, они дают лучшие результаты, чем англоязычные или многоязычные варианты.
12.5.1 Reticulate
Для работы с трансформерами понадобится Python. Создадим виртуальное окружение, которое нужно для корректной работы с пакетом {text}.
library(reticulate)
use_python("/usr/bin/python3")py_config()
# python: /usr/bin/python3
# libpython: /Library/Developer/CommandLineTools/Library/Frameworks/Python3.framework/Versions/3.9/lib/python3.9/config-3.9-darwin/libpython3.9.dylib
# pythonhome: /Library/Developer/CommandLineTools/Library/Frameworks/Python3.framework/Versions/3.9:/Library/Developer/CommandLineTools/Library/Frameworks/Python3.framework/Versions/3.9
# version: 3.9.6 (default, Feb 3 2024, 15:58:27) [Clang 15.0.0 (clang-1500.3.9.4)]
# numpy: /Users/olga/Library/Python/3.9/lib/python/site-packages/numpy
# numpy_version: 1.23.0
#
# NOTE: Python version was forced by use_python() functionpy_eval("1+1")Для работы понадобятся модули nltk и transformers. Проверьте в терминале, установлены ли они, и, если надо, установите.
# проверить
/usr/bin/python3 -c "import nltk; print('nltk version:', nltk.__version__)"
/usr/bin/python3 -c "import transformers; print('transformers version:', transformers.__version__)"
# установить
/usr/bin/python3 -m pip install nltk transformersСкачайте необходимые данные для NLTK.
py_run_string("
import nltk
nltk.download('punkt')
nltk.download('punkt_tab')
nltk.download('stopwords')
nltk.download('wordnet')
nltk.download('omw-1.4')
")12.5.2 Эмбеддинги
Получаем эмбеддинги с помощью textEmbed(). Это долго (для нашего датасета около двух часов). Для пробы берем лишь несколько новостей.
set.seed(18112025)
news_sample <- news_2019 |>
filter(topic %in% c("Экономика", "Культура", "Спорт")) |>
sample_n(size = 25)Во время обучения вы увидите предупреждение о non-ASCII символах. Если ваша модель обучена на русском или многоязычная, это предупреждение можно игнорировать.
emb <- textEmbed(
texts = news_sample$text,
# или другая модель
model = "cointegrated/rubert-tiny2",
# по умолчанию
layers = -2,
remove_non_ascii = FALSE
)Получаем эмбеддинги для токенов. 313 - размерность эмбеддинга для каждого токена. BERT-токенизатор использует WordPiece токенизацию, которая разбивает слова на субтокены. Это позволяет обрабатывать редкие и неизвестные слова.
emb$tokens$texts[[2]] Токен [CLS] (=classification) — это специальный служебный токен BERT (и его производных моделей), который автоматически добавляется в самое начало каждого входного текста.
emb$texts$texts12.5.3 2D-визуализации
emb_texts <- emb$texts$texts |>
mutate(text_id = news_sample$id) |>
mutate(topic = news_sample$topic)
umap_res <- emb_texts |>
dplyr::select(-text_id, -topic) |>
as.matrix() |>
umap(n_neighbors = 15, min_dist = 0.1, metric = "cosine")
plot_df <- as.data.frame(umap_res) |>
setNames(c("UMAP1", "UMAP2")) |>
mutate(text_id = emb_texts$text_id,
topic = emb_texts$topic)
plot_df |>
ggplot(aes(UMAP1, UMAP2, color = topic)) +
geom_text(aes(label = text_id), alpha = 0.8, size = 3) +
theme_minimal()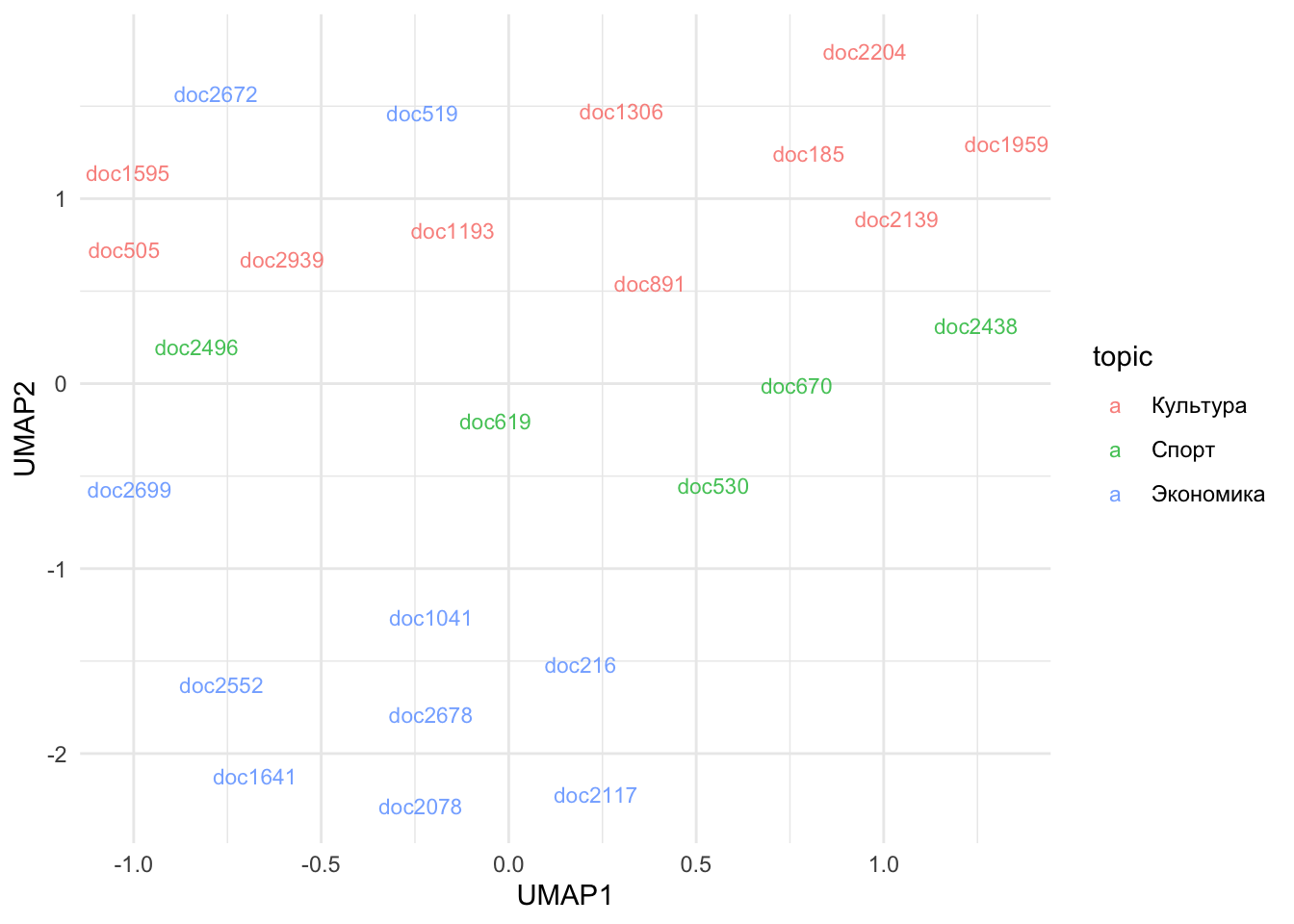
Doc2672 содержит новость о дочери актера, а doc519 – о рейтинге самых высокооплачиваемых иллюзионистов.
12.5.4 Ближайшие соседи
nearest_neighbors_matrix <- function(df, feat_row) {
# df: датафрейм или матрица, в каждой строке эмбеддинг
# feat_row: индекс строки/имя строки, для которой ищем соседа
m <- as.matrix(df)
# вектор-эмбеддинг выбранного текста
v <- m[feat_row, ]
# косинусное сходство
similarities <- (m %*% v) / (sqrt(rowSums(m^2)) * sqrt(sum(v^2)))
# самого себя не берём
similarities[feat_row] <- -Inf
# ближайший – максимальное сходство
nn_idx <- which.max(similarities)
# выводим результат
list(
index = nn_idx,
similarity = similarities[nn_idx]
)
}nn <- nearest_neighbors_matrix(df = emb_texts %>% dplyr::select(-text_id, -topic), feat_row = 5)
nn$index
[1] 21
$similarity
[1] 0.949336news_sample |>
filter(row_number() == 5) |>
pull(text)[1] "Российская рок-группа «Браво» выступит в Москве в новогоднюю ночь. Об этом сообщается в пресс-релизе, поступившем в редакцию «Ленты.ру». Концерт начнется после полуночи в клубе «16 Тонн». Отмечается, что на мероприятии прозвучат все хиты коллектива, включая такие песни, как «Московский бит», «Старый отель», «Любите девушки», «Верю я», «Дорога в облака», «Этот город», «Ветер знает» и «Любовь не горит». Кроме того, на двух этажах клуба будут работать танцполы с диджеями. Билеты на концерт можно приобрести на сайте площадке. В их стоимость будет включено не только посещения праздника, но и все блюда из новогоднего меню. Группа «Браво» была основана Евгением Хавтаном в 1983 году. Солистами коллектива в разные годы были Жанна Агузарова, Валерий Сюткин и Роберт Ленц. Во время новогодних праздников в клубе «16 тонн» выступят и такие артисты, как «Рекорд Оркестр» (1 января), «НОМ» (2 января), Андрей Князев (3 января), On-the-Go (4 января), Найк Борзов (6 января), Zero People (7 января) и «Буерак» (8 января)."news_sample |>
filter(row_number() == nn$index) |>
pull(text)[1] "Группа «Алиса» даст традиционный концерт в день рождения фронтмена Константина Кинчева. Об этом сообщается в пресс-релизе, поступившем в редакцию «Ленты.ру». Отмечается, что выступление состоится 28 декабря в московском клубе «Известия Hall». На таких мероприятиях коллектив, как правило, исполняет «внепрограмнные» песни, которые редко звучат со сцены. Билеты можно приобрести на сайте. Группа« Алиса» была образована в 1983 году в Ленинграде. С тех пор она записала более 20 альбомов. Автором многих песен коллектива является Константин Кинчев, который стал вокалистом «Алисы» в 1984 году. За время своего существования в группе сменилось около десятка разных музыкантов. Кинчев вместе с остальными участниками «Алисы» создал такие альбомы, как «Энергия», «Блок ада», «Шестой лесничий», «Черная метка», «Солнцеворот» и другие."