Тема 16 Сетевые данные и графы

Сети – это все, что окружает нас.

Люк (2017)

Любые сети состоят из отдельных участников (людей или вещей в сети) и отношений между ними. Сети очень часто визуализируются с помощью графов – структур, состоящих из множества точек и линий, отображающих связи между этими точками. Участники представлены в виде узлов сети, а их отношения представлены в виде линий, их связывающих55.

Пример исследования сетей соавторства на ФГН НИУ ВШЭ. Это исследование было предметом оживленной дискуссии, частично опубликованной на сайте ВШЭ.

16.1 Базовое описание

Мы начнем работу с сетями на небольшом датасете, опубликованном Якобом Морено в 1930-х гг. Этот датасет содержит сеть дружеских отношений между учениками 4-го класса.

library(network)
library(sna)
# devtools::install_github("DougLuke/UserNetR")
library(UserNetR)
data("Moreno")
summary(Moreno, print.adj = F)
## Network attributes:
##   vertices = 33
##   directed = FALSE
##   hyper = FALSE
##   loops = FALSE
##   multiple = FALSE
##   bipartite = FALSE
##  total edges = 46 
##    missing edges = 0 
##    non-missing edges = 46 
##  density = 0.08712121 
## 
## Vertex attributes:
## 
##  gender:
##    numeric valued attribute
##    attribute summary:
##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##   1.000   1.000   2.000   1.515   2.000   2.000 
##   vertex.names:
##    character valued attribute
##    33 valid vertex names
## 
## No edge attributes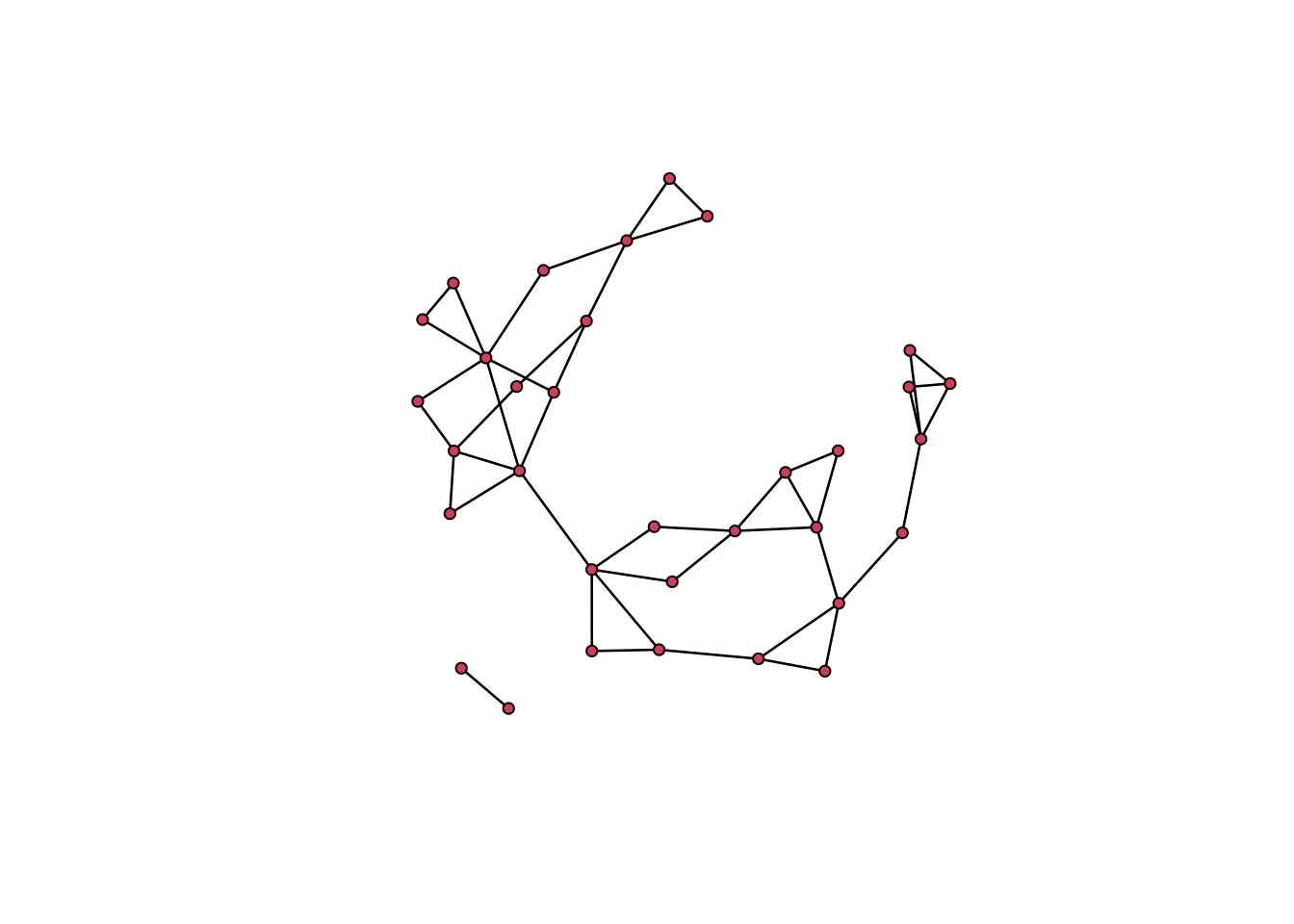
plot(Moreno)

Самая главная характеристика сети – это ее размер. Размер – это количество участников (members), которые называются узлами (nodes), вершинами (vertices) или акторами.

network.size(Moreno)
## [1] 33

Еще одна важная характеристика сети – это ее плотность.

gden(Moreno)
## [1] 0.08712121

Плотность – это доля имеющихся связей по отношению к максимально возможному количеству связей. Формула плотности будет отличаться для направленных (\(\frac{L}{k(k - 1)}\)) и ненаправленных (\(\frac{2L}{k(k-1)}\)) сетей (где \(k(k-1)\) – это максимально возможное число связей).

Компонента сети – это подгруппа, где все акторы связаны между собой прямо или косвенно. На графе выше видно две компоненты.

Диаметр сети – количество шагов, которые нужно пройти, чтобы попасть из узла А в узел B; для сетей с несколькими компонентами учитывается та, что больше. Геодезическое расстояние – это кратчайший путь между двумя узлами; диаметром считается максимальное расстояние для двух узлов.

lgc <- component.largest(Moreno, result = "graph")
gd <- geodist(lgc)
max(gd$gdist)
## [1] 11

Коэффициент кластеризации, или транзитивность, отражает тенденцию к созданию закрытых треугольников, т.е. к замыканию. Транзитивность определяется как доля закрытых треугольников по отношению к общему количеству открытых и закрытых треугольников.

gtrans(Moreno, mode="graph")
## [1] 0.2857143

16.2 Создание сетевых данных

16.2.1 Социоматрица

Матрица, хранящая информацию о сети, называется социоматрицей (или матрицей смежности). Ее можно создать вручную.

netmat1 <- rbind(c(0,1,1,0,0),
                 c(0,0,1,1,0),
                 c(0,1,0,0,0),
                 c(0,0,0,0,0),
                 c(0,0,1,0,0))
rownames(netmat1) <- letters[1:5]
colnames(netmat1) <- letters[1:5]
net1 <- network(netmat1, matrix.type ="adjacency")
class(net1)
## [1] "network"
summary(net1)
## Network attributes:
##   vertices = 5
##   directed = TRUE
##   hyper = FALSE
##   loops = FALSE
##   multiple = FALSE
##   bipartite = FALSE
##  total edges = 6 
##    missing edges = 0 
##    non-missing edges = 6 
##  density = 0.3 
## 
## Vertex attributes:
##   vertex.names:
##    character valued attribute
##    5 valid vertex names
## 
## No edge attributes
## 
## Network adjacency matrix:
##   a b c d e
## a 0 1 1 0 0
## b 0 0 1 1 0
## c 0 1 0 0 0
## d 0 0 0 0 0
## e 0 0 1 0 0

Функция gplot из пакета sna позволяет визуализировать эту матрицу в виде графа.

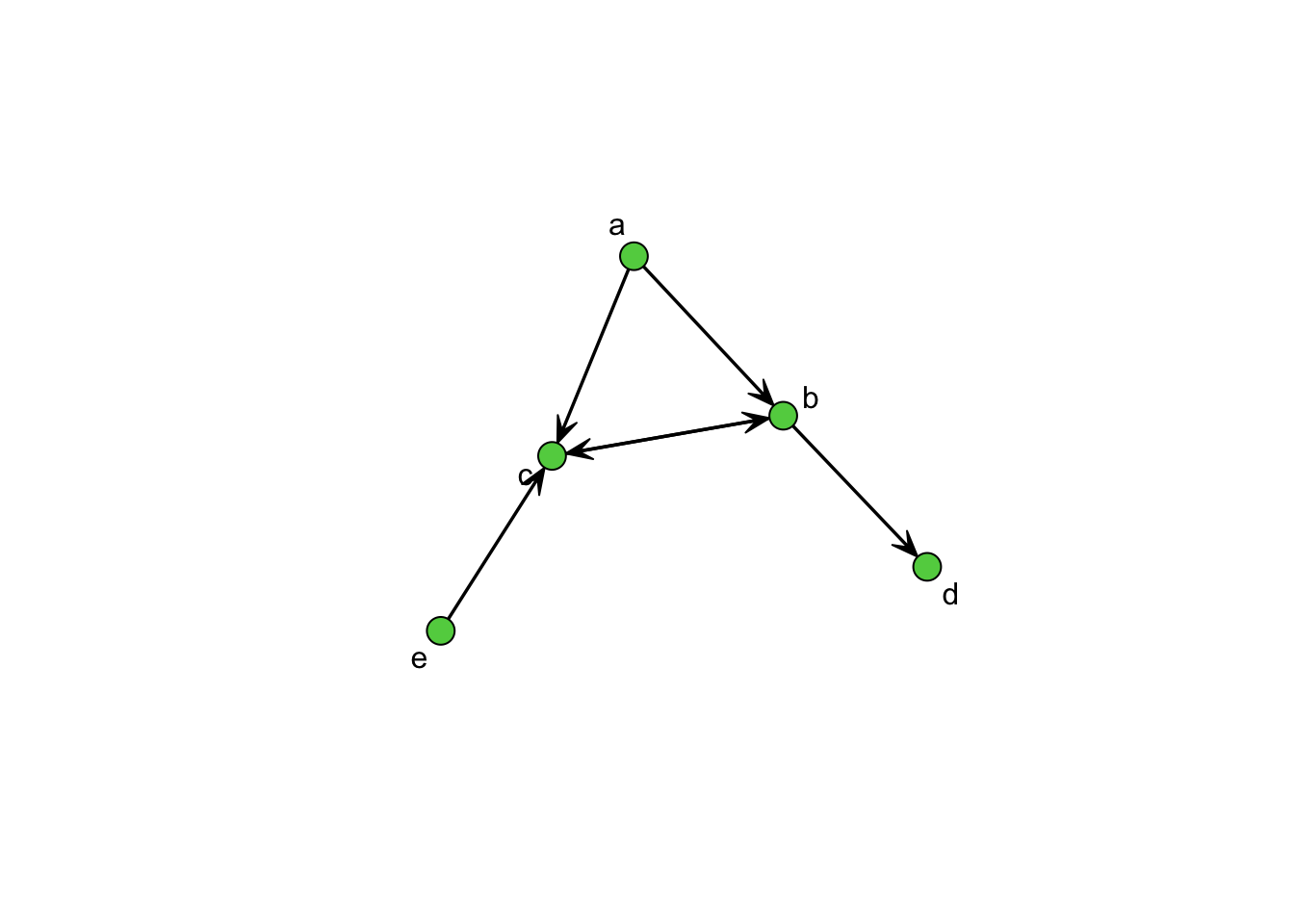
gplot(net1, vertex.col = 3, displaylabels = TRUE)

16.2.2 Список ребер

Ту же матрицу можно построить при помощи списка ребер. Списки ребер меньше по размеру, и собирать сетевые данные в таком формате проще.

netmat2 <- rbind(c(1,2),
                 c(1,3),
                 c(2,3),
                 c(2,4),
                 c(3,2),
                 c(5,3))
net2 <- network(netmat2, matrix.type = "edgelist")
network.vertex.names(net2) <- letters[1:5]
summary(net2)
## Network attributes:
##   vertices = 5
##   directed = TRUE
##   hyper = FALSE
##   loops = FALSE
##   multiple = FALSE
##   bipartite = FALSE
##  total edges = 6 
##    missing edges = 0 
##    non-missing edges = 6 
##  density = 0.3 
## 
## Vertex attributes:
##   vertex.names:
##    character valued attribute
##    5 valid vertex names
## 
## No edge attributes
## 
## Network adjacency matrix:
##   a b c d e
## a 0 1 1 0 0
## b 0 0 1 1 0
## c 0 1 0 0 0
## d 0 0 0 0 0
## e 0 0 1 0 0

Граф будет выглядеть точно так же.

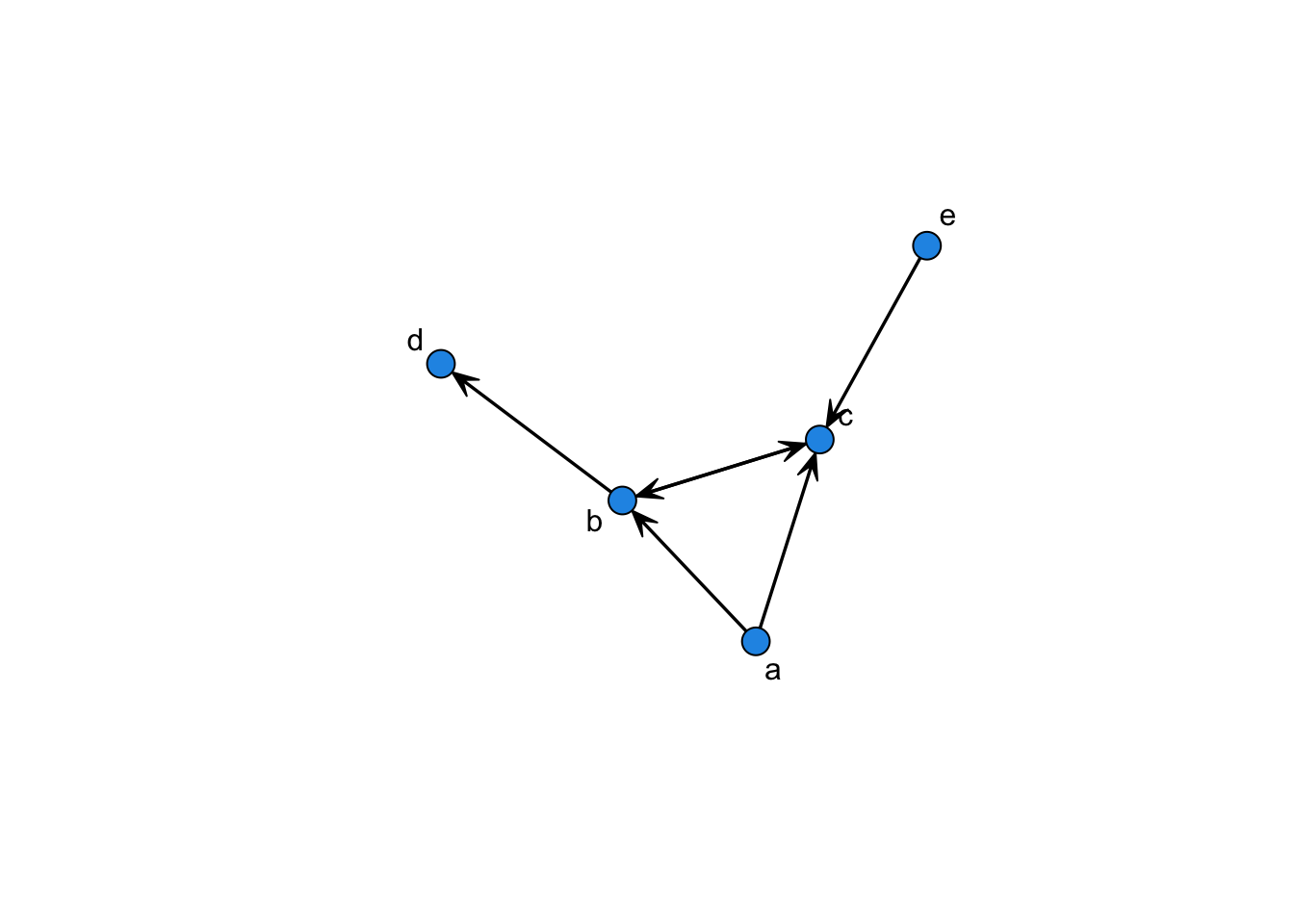
gplot(net2, vertex.col = 4, displaylabels = TRUE)

16.2.3 Формула

Пакет igraph дает возможность создать сеть разными способами, в том числе с использованием формулы. Перед использованием пакета лучше отвязать statnet. Для ненаправленных графов используется --, для направленных -+.

detach(package:sna)
detach(package:network)
library(igraph)
g <- graph.formula(a--c, a--b, b--d, b--c, e--c)
g
## IGRAPH 9b980d2 UN-- 5 5 -- 
## + attr: name (v/c)
## + edges from 9b980d2 (vertex names):
## [1] a--c a--b c--b c--e b--d

Объекты igraph можно передать напрямую plot56, но ниже мы рассмотрим и другие возможности.

plot(g)

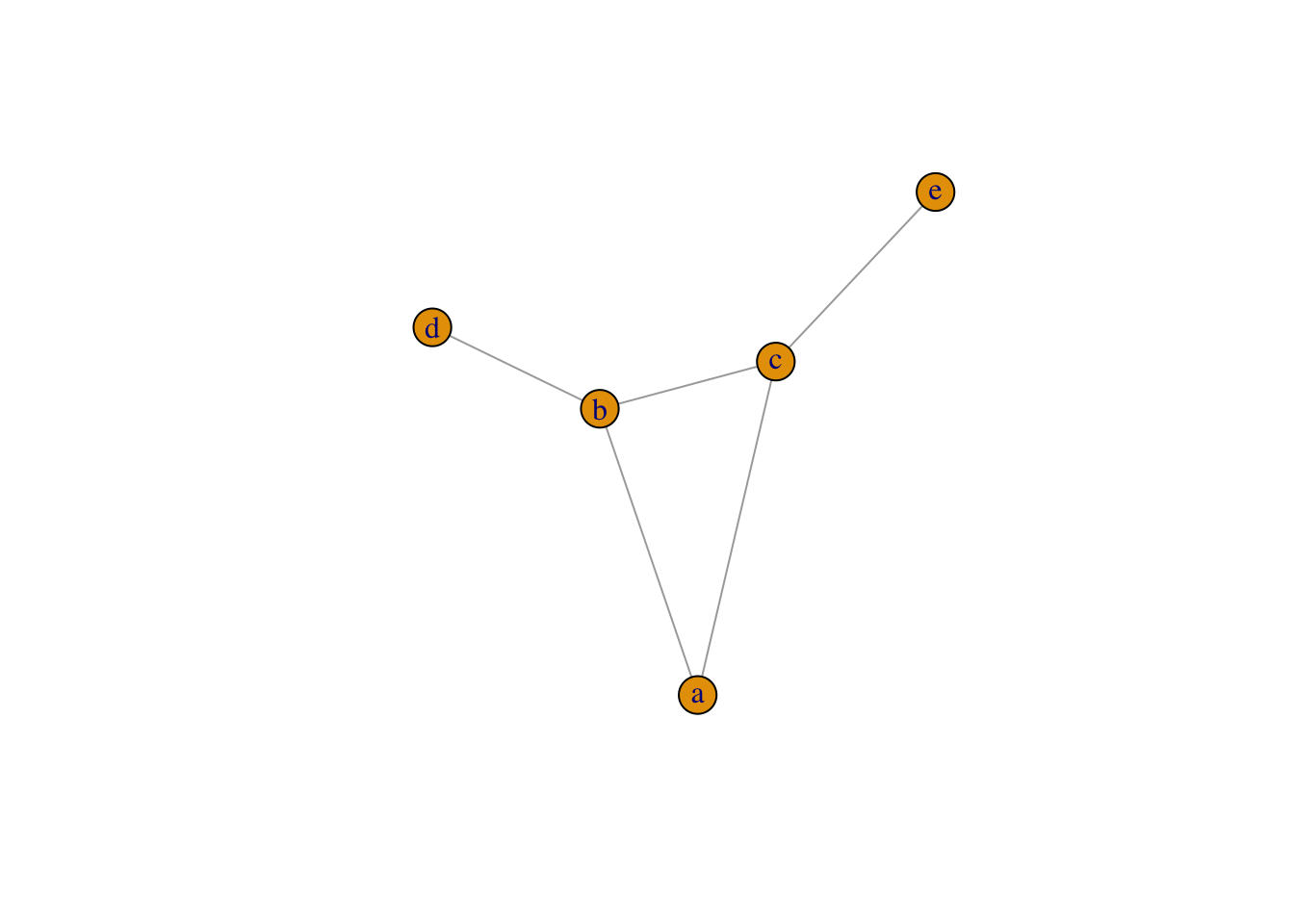
16.2.4 Импорт данных

Также данные можно импортировать. Мы воспользуемся датасетом, опубликованном на сайте Пушкинского дома, “Словарь русских писателей XVIII века: сеть персоналий”.

Датасет представляет собой осмысленные в терминах сетевого анализа междустатейные ссылки в Словаре русских писателей XVIII века (1988–2010. Вып. 1–3). Узлами сети выступают посвященные персоналиям статьи словаря, а ребрами — ссылки на другие статьи в том же словаре.

library(readr)
dict_data <- read_csv(file = "files/Persons_EDGES.csv")

dict_data
## # A tibble: 4,440 × 4
##    Source       Target            Weight Type    
##    <chr>        <chr>              <dbl> <chr>   
##  1 Н.И.Ахвердов П.И.Богданович         1 directed
##  2 А.Д.Байбаков А.А.Барсов             1 directed
##  3 А.Д.Кантемир А.К.Барсов             1 directed
##  4 А.Д.Кантемир С.С.Волчков            1 directed
##  5 А.Д.Кантемир И.И.Ильинский          1 directed
##  6 А.Д.Кантемир Ф.Кролик               1 directed
##  7 А.Д.Кантемир М.В.Ломоносов          1 directed
##  8 А.Д.Кантемир Е.Прокопович           1 directed
##  9 А.Д.Кантемир А.П.Сумароков          1 directed
## 10 А.Д.Кантемир В.К.Тредиаковский      1 directed
## # ℹ 4,430 more rows

Эту таблицу можно преобразовать в сеть несколькими способами. Функция graph_from_edgelist() ожидает на входе матрицу с двумя столбцами.

dict_graph <- graph_from_edgelist(as.matrix(dict_data[,1:2]))

summary(dict_graph, print.adj = F)
## IGRAPH b8694e2 DN-- 780 4440 -- 
## + attr: name (v/c)

Описание позволяет понять, что граф является направленным (D), а его узлы имеют имена (N). Всего в графе 780 вершин и 4440 связей. Демонстрационная версия интерактивного приложения, построенного на сетевых данных, размещена здесь. Приложение позволяет работать с отдельными узлами сети, изучать их соседей и количественные характеристики. Мы же выведем лишь небольшую часть узлов.

16.3 Атрибуты вершин (узлов)

В том же объекте-сети можно хранить дополнительные данные об узлах. В датасете “Словарь…” в качестве такого атрибута хранятся данные об имени автора:

names <- names(V(dict_graph))
names[1:12]
##  [1] "Н.И.Ахвердов"   "П.И.Богданович" "А.Д.Байбаков"  
##  [4] "А.А.Барсов"     "А.Д.Кантемир"   "А.К.Барсов"    
##  [7] "С.С.Волчков"    "И.И.Ильинский"  "Ф.Кролик"      
## [10] "М.В.Ломоносов"  "Е.Прокопович"   "А.П.Сумароков"

Атрибуты вершин можно использовать для того, чтобы задать новую подсеть для анализа. Например, выбрать только некоторых авторов из “Словаря…”.

vert <- which(names(V(dict_graph)) %in% c("Д.И.Фонвизин", "А.Д.Кантемир", "В.К.Тредиаковский", "Е.Р.Дашкова", "Н.М.Карамзин"))

dict_sub <- induced_subgraph(dict_graph, 
                             vids = vert)

dict_sub
## IGRAPH cdf73ff DN-- 5 8 -- 
## + attr: name (v/c)
## + edges from cdf73ff (vertex names):
## [1] А.Д.Кантемир     ->В.К.Тредиаковский
## [2] В.К.Тредиаковский->А.Д.Кантемир     
## [3] В.К.Тредиаковский->Н.М.Карамзин     
## [4] В.К.Тредиаковский->Д.И.Фонвизин     
## [5] Н.М.Карамзин     ->В.К.Тредиаковский
## [6] Д.И.Фонвизин     ->В.К.Тредиаковский
## [7] Д.И.Фонвизин     ->Н.М.Карамзин     
## [8] Д.И.Фонвизин     ->Е.Р.Дашкова

16.4 Фильтрация по узлу

Для визуализации таких объектов подходит функция ggraph() из одноименного пакета, которая основана на грамматике ggplot.

library(ggraph)
names <- names(V(dict_sub))

ggraph(dict_sub, layout = "fr") +
  geom_edge_link(color = "cadetblue3") +
  geom_node_point(size = 5, color = "bisque4", shape = 18) +
  geom_node_text(aes(label = names), nudge_y = -0.1) +
  theme_graph()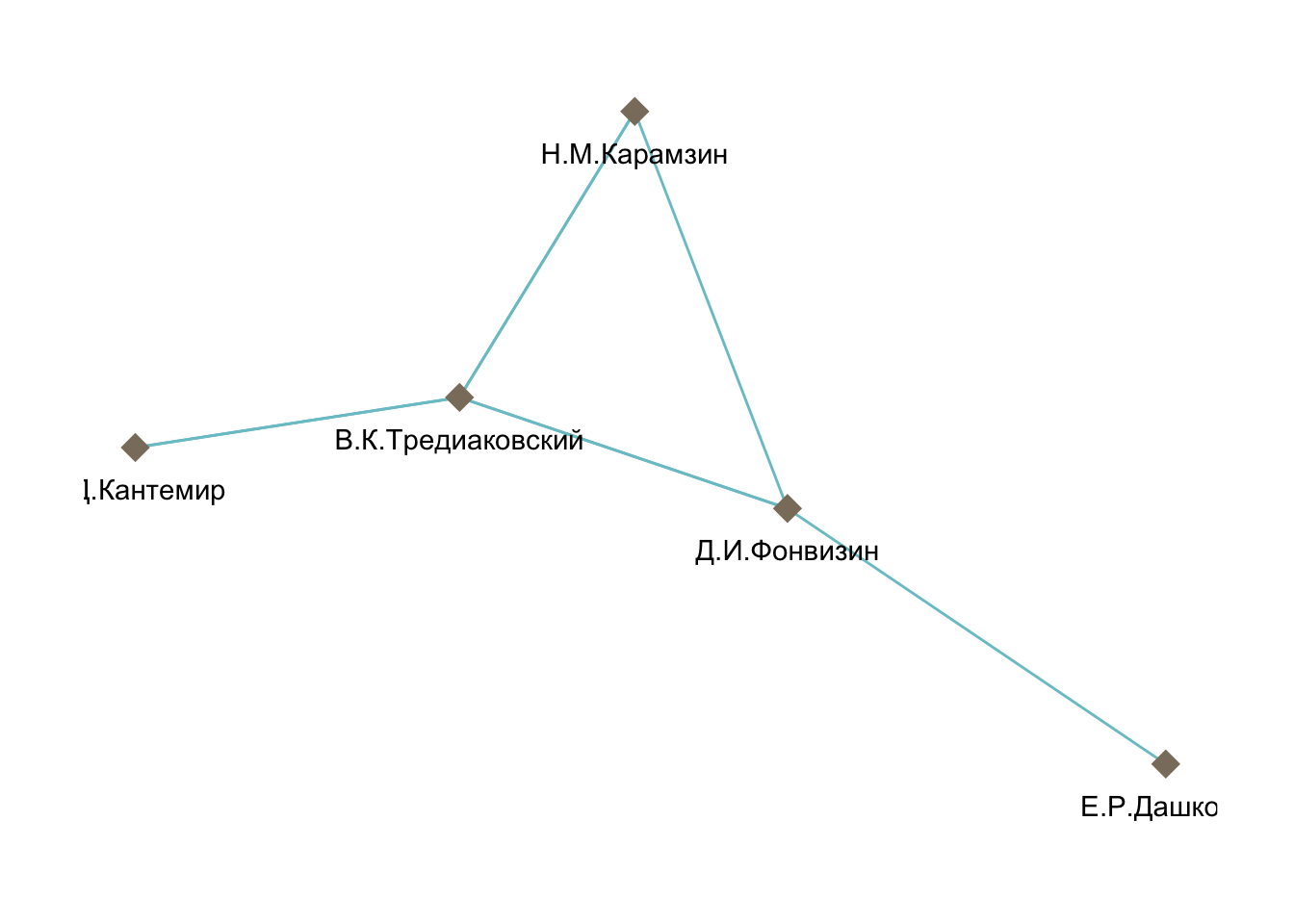

Немного баловства (но лучше, конечно, другие картинки использовать).

library(ggimage)
## 
## Attaching package: 'ggimage'
## The following object is masked from 'package:cowplot':
## 
##     theme_nothing
## получаем координаты
subgraph.layout <- layout.fruchterman.reingold(dict_sub)
x <-  subgraph.layout[,1]
y <- subgraph.layout[,2]

ggraph(dict_sub, layout = subgraph.layout) +
  geom_edge_link(color = "cadetblue3") +
  geom_pokemon(aes(x, y), image="pikachu", size = 0.2) +
  geom_node_text(aes(label = names), nudge_y = -0.1) +
  theme_graph()

Теперь выберем отдельный узел вместе с его соседями.

vert <- which(names(V(dict_graph))=="А.Д.Кантемир")

dict_sub <- induced_subgraph(dict_graph, 
                             vids = c(vert, neighbors(dict_graph, "А.Д.Кантемир")))
dict_sub
## IGRAPH 73bcc73 DN-- 9 30 -- 
## + attr: name (v/c)
## + edges from 73bcc73 (vertex names):
##  [1] А.Д.Кантемир ->А.К.Барсов       
##  [2] А.Д.Кантемир ->С.С.Волчков      
##  [3] А.Д.Кантемир ->И.И.Ильинский    
##  [4] А.Д.Кантемир ->Ф.Кролик         
##  [5] А.Д.Кантемир ->М.В.Ломоносов    
##  [6] А.Д.Кантемир ->Е.Прокопович     
##  [7] А.Д.Кантемир ->А.П.Сумароков    
##  [8] А.Д.Кантемир ->В.К.Тредиаковский
## + ... omitted several edges

Используем другую укладку, также повернем и сдвинем подписи.

names <- names(V(dict_sub))

ggraph(dict_sub, layout = "linear") +
  geom_edge_arc(color = "cadetblue3") +
  geom_node_point(size = 5, color = "bisque4", shape = 18) +
  geom_node_text(aes(label = names), angle = 60, nudge_x = 0.1, nudge_y = -0.1) +
  theme_graph()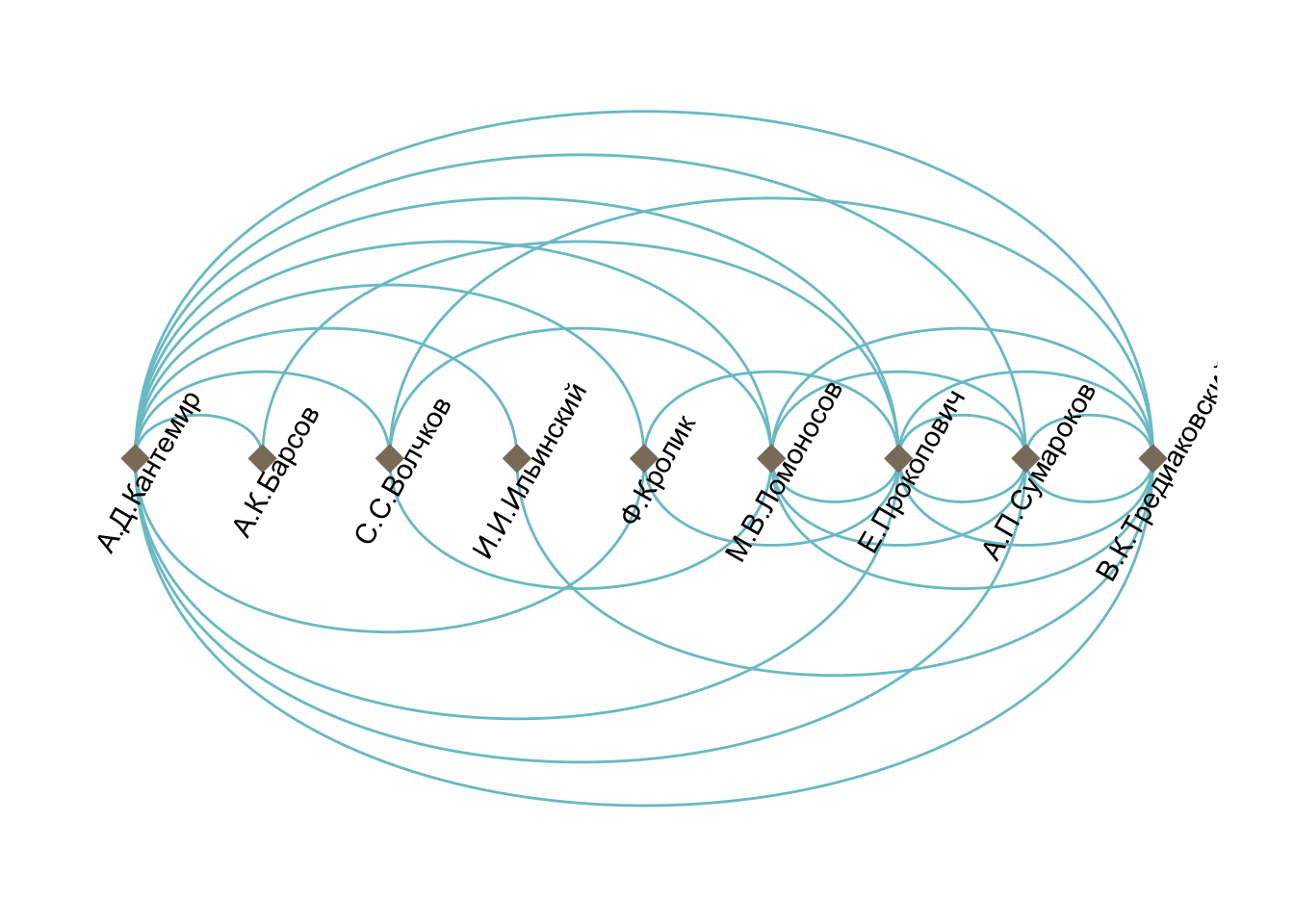

16.5 Атрибуты ребер

В данных из “Словаря…” у ребер нет атрибутов, в чем легко убедиться.

get.edge.attribute(dict_sub)
## named list()

В некоторых случаях бывает полезно эти атрибуты назначить: например, если вы провели дополнительное исследование и хотите добавить данные.

set.seed(1234)
dict_sub <- set_edge_attr(dict_sub, "value", index = E(dict_sub), value = sample(1:3, length(E(dict_sub)), replace = T))

Назначенный атрибут (сейчас это случайное число) можно закодировать на графе:

ggraph(dict_sub, layout = "linear") +
  geom_edge_arc(aes(width = value), color = "cadetblue3", alpha = 0.5) +
  geom_node_point(size = 5, color = "bisque4", shape = 18) +
  geom_node_text(aes(label = names), angle = 60, nudge_x = 0.1, nudge_y = -0.1) +
  theme_graph()

16.6 Импорт из gexf

Датасет “«Камер-фурьерский журнал» В. Ходасевича” хранит информацию о встречах, которые В. Ходасевич фиксировал в своем камер-фурьерском журнале, начиная с 1922 года. Данные за каждый месяц хранятся отдельно в файлах формата gexf (Graph Exchange XML Format)), для их чтения нужен особый пакет.

library(rgexf)
kfj <- read.gexf("files/1922_Июль_.gexf")
head(kfj)
## <?xml version="1.0" encoding="UTF-8"?>
## <gexf xmlns="http://www.gexf.net/1.1draft" xmlns:viz="http://www.gexf.net/1.1draft/viz" xmlns:xsi="http://www.w3.org/2001/XMLSchema-instance" version="1.1" xsi:schemaLocation="http://www.w3.org/2001/XMLSchema-instance">
##   <graph defaultedgetype="undirected" mode="static">
##     <nodes>
##       <node id="Туся" label="Туся"/>
##       <node id="Минский" label="Минский"/>
##       <node id="Шаляпин" label="Шаляпин"/>
##       <node id="Женя" label="Женя"/>
##       <node id="Толстой" label="Толстой"/>
##       <node id="Эренбург" label="Эренбург"/>
##       <node id="Нина" label="Нина"/>
##       <node id="Белый" label="Белый"/>
##       <node id="Добровейн" label="Добровейн"/>
##       <node id="Горький" label="Горький"/>
##       <node id="Феррари" label="Феррари"/>
##       <node id="Ася" label="Ася"/>
##       <node id="Парнах" label="Парнах"/>
##       <node id="Кусиков" label="Кусиков"/>
##       <node id="Зайцева_В" label="Зайцева_В"/>
##       <node id="Залшупин" label="Залшупин"/>
##       <node id="Кречетов" label="Кречетов"/>
##       <node id="Шкловский" label="Шкловский"/>
##       <node id="Каплун_Б" label="Каплун_Б"/>
##       <node id="Берберов_Л" label="Берберов_Л"/>
##       <node id="Венгерова" label="Венгерова"/>
##       <node id="Маковский" label="Маковский"/>
##       <node id="Рындина" label="Рындина"/>
##       <node id="Багратион-Мухранская" label="Багратион-Мухранская"/>
##       <node id="Цветаева" label="Цветаева"/>
##       <node id="Ященко" label="Ященко"/>
##       <node id="Юренева" label="Юренева"/>
##       <node id="Дроздов" label="Дроздов"/>
##       <node id="Горный" label="Горный"/>
##       <node id="Григорович" label="Григорович"/>
##       <node id="Берберов" label="Берберов"/>
##       <node id="Вишняк" label="Вишняк"/>
##       <node id="Постников" label="Постников"/>
##       <node id="Пуни" label="Пуни"/>
##       <node id="Слоним" label="Слоним"/>
##       <node id="Амфитеатров" label="Амфитеатров"/>
##       <node id="Зайцев_Б" label="Зайцев_Б"/>
##       <node id="Пешков_М" label="Пешков_М"/>
##       <node id="Алянский" label="Алянский"/>
##       <node id="Андреева" label="Андреева"/>
##       <node id="Каплун" label="Каплун"/>
##       <node id="Ракицкий" label="Ракицкий"/>
##          ...
##      </nodes>
##     <edges>
##       <edge id="0" source="Туся" target="Толстой" weight="1"/>
##       <edge id="1" source="Минский" target="Кусиков" weight="1"/>
##       <edge id="2" source="Минский" target="Юренева" weight="1"/>
##       <edge id="3" source="Минский" target="Эренбург" weight="1"/>
##       <edge id="4" source="Минский" target="Шкловский" weight="1"/>
##       <edge id="5" source="Минский" target="Постников" weight="1"/>
##          ...
##      </edges>
##   </graph>
## </gexf>

Трансформируем в формат igraph.

kfj_graph <- gexf.to.igraph(kfj)
kfj_graph
## IGRAPH 0f74e8e UNW- 42 86 -- 
## + attr: layout (g/n), name (v/c), color (v/c), size (v/n),
## | weight (e/n)
## + edges from 0f74e8e (vertex names):
##  [1] Толстой             --Туся     
##  [2] Кусиков             --Минский  
##  [3] Минский             --Юренева  
##  [4] Минский             --Эренбург 
##  [5] Минский             --Шкловский
##  [6] Минский             --Постников
##  [7] Венгерова           --Минский  
## + ... omitted several edges

В данном случае U означает ненаправленный граф, а N говорит о том, что вершины имеют имена. Буква W указывает на то, что ребрам присвоены веса. Далее приводится информация о количестве вершин (42) и ребер (86).

Заглянем в атрибуты.

# имена узлов 
V(kfj_graph) 
## + 42/42 vertices, named, from 0f74e8e:
##  [1] Алянский             Амфитеатров          Андреева            
##  [4] Ася                  Багратион-Мухранская Белый               
##  [7] Берберов             Берберов_Л           Венгерова           
## [10] Вишняк               Горный               Горький             
## [13] Григорович           Добровейн            Дроздов             
## [16] Женя                 Зайцев_Б             Зайцева_В           
## [19] Залшупин             Каплун               Каплун_Б            
## [22] Кречетов             Кусиков              Маковский           
## [25] Минский              Нина                 Парнах              
## [28] Пешков_М             Постников            Пуни                
## + ... omitted several vertices

Сохраним имена узлов как вектор.

names <- get.vertex.attribute(kfj_graph)$name

Зачем-то в объекте хранится еще и цвет узлов (один для всех).

color <- V(kfj_graph)$color
color
##  [1] "#FF6347FF" "#FF6347FF" "#FF6347FF" "#FF6347FF" "#FF6347FF"
##  [6] "#FF6347FF" "#FF6347FF" "#FF6347FF" "#FF6347FF" "#FF6347FF"
## [11] "#FF6347FF" "#FF6347FF" "#FF6347FF" "#FF6347FF" "#FF6347FF"
## [16] "#FF6347FF" "#FF6347FF" "#FF6347FF" "#FF6347FF" "#FF6347FF"
## [21] "#FF6347FF" "#FF6347FF" "#FF6347FF" "#FF6347FF" "#FF6347FF"
## [26] "#FF6347FF" "#FF6347FF" "#FF6347FF" "#FF6347FF" "#FF6347FF"
## [31] "#FF6347FF" "#FF6347FF" "#FF6347FF" "#FF6347FF" "#FF6347FF"
## [36] "#FF6347FF" "#FF6347FF" "#FF6347FF" "#FF6347FF" "#FF6347FF"
## [41] "#FF6347FF" "#FF6347FF"

Атбрибуты ребер.

weight <- get.edge.attribute(kfj_graph)$weight
weight
##  [1] 1 1 1 1 1 1 3 1 1 1 1 1 1 1 1 2 1 1 1 1 1 2 1 1 1 1 1 1 1 1 1
## [32] 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 1 1 1 1
## [63] 1 1 1 1 1 1 1 1 1 1 3 1 1 1 1 1 1 1 1 1 1 1 1 1

16.7 Визуализация с ggraph

Ширину ребра отрегулируем в зависимости от веса, который отражает частоту контактов. Мы уже видели, что эти данные хранятся в атрибутах ребер. Функция as.factor препятствует дроблению чисел, т.к. в нашем случае это не имеет смысла.

ggraph(kfj_graph) +
  geom_edge_link(alpha = 0.25, 
                   aes(width = as.factor(weight)), 
                   show.legend = F) +
  geom_node_point(color = color, show.legend = F, size = 2) +
  geom_node_text(aes(label = names),  repel = TRUE) +
  theme_graph()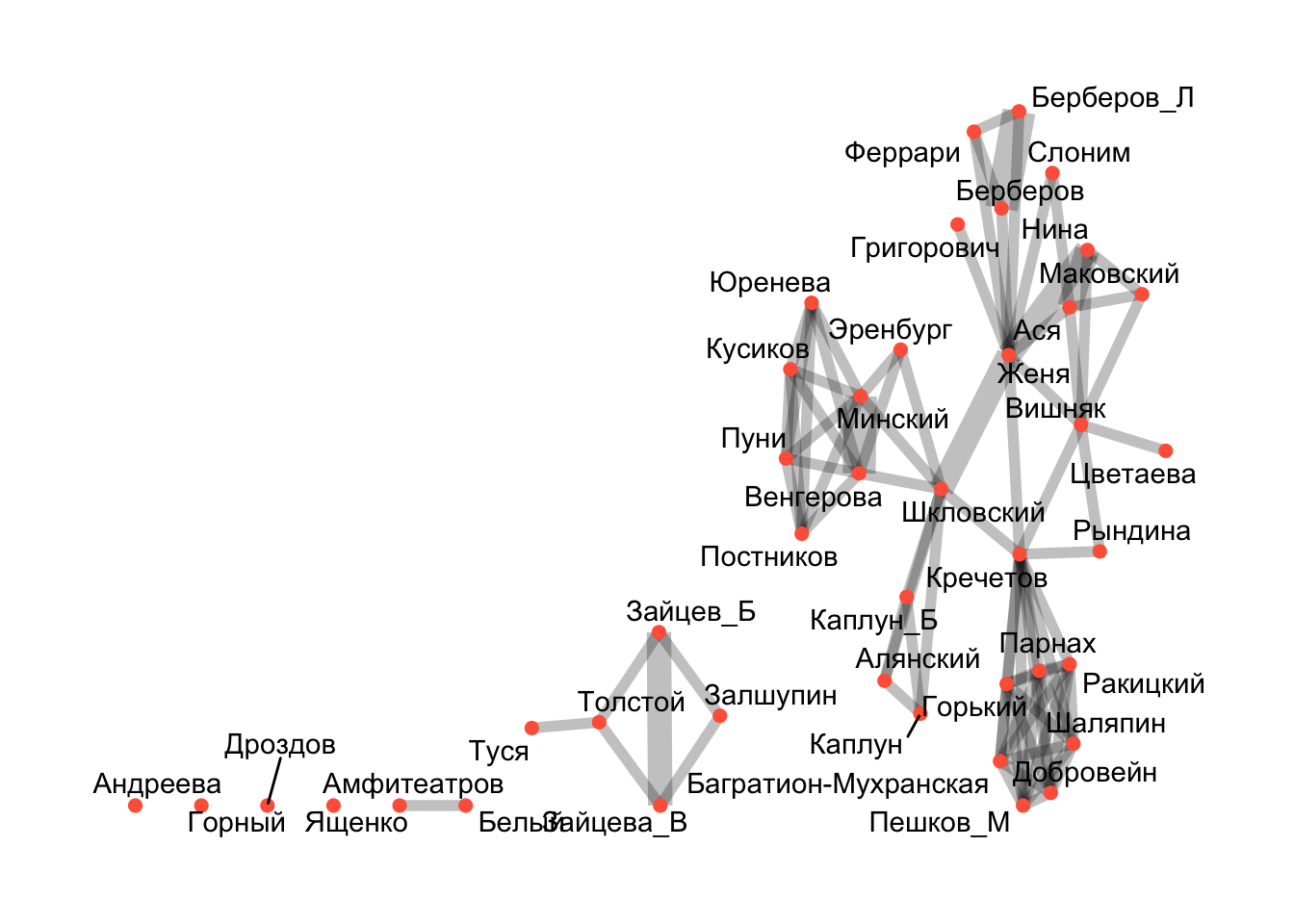

16.8 Фильтрация по атрибутам ребер

Атрибуты ребер, как и атрибуты имен, можно использовать для создания подсети. Например, мы можем отобрать только имена тех людей, с которыми Ходасевич встречался больше одного раза в месяц (это август 1922 г.).

E(kfj_graph)[weight > 1]
## + 6/86 edges from 0f74e8e (vertex names):
## [1] Венгерова--Минский    Женя     --Нина      
## [3] Женя     --Шкловский  Ася      --Нина      
## [5] Зайцев_Б --Зайцева_В  Берберов --Берберов_Л

Визуализируем подсеть. Цветовая раскраска в данном случае ничего не добавляет, просто показываю красивое. Подписи можно добавить не только к узлам, но и к ребрам.

kfj_sub <- subgraph.edges(kfj_graph, E(kfj_graph)[weight > 1])
names_sub <- get.vertex.attribute(kfj_sub)$name
weight_sub <- get.edge.attribute(kfj_sub)$weight

ggraph(kfj_sub, layout = "kk") +
  geom_edge_link(alpha = 0.25, 
                 linetype = 2, 
                 aes(label = weight_sub), 
                 label_colour = "sienna", 
                 label_dodge = unit(2.5, 'mm'),
                 angle_calc = 'along') +
  geom_node_point(size = 3, aes(color = names_sub), show.legend = F) +
  geom_node_text(aes(label = names_sub),  repel = TRUE) +
  theme_graph()

16.9 Укладка сети

Графическое представление одной и той же сети будет зависеть от выбранного способа укладки.

При построении графиков сетей стремятся следовать следующим принципам:

  • минимизировать пересечения ребер;
  • максимизировать симметричность укладки узлов;
  • минимизировать изменчивость длины ребер;
  • максимизировать угол между ребрами, когда они пересекают или соединяют узлы;
  • минимизировать общее пространство для вывода сети.

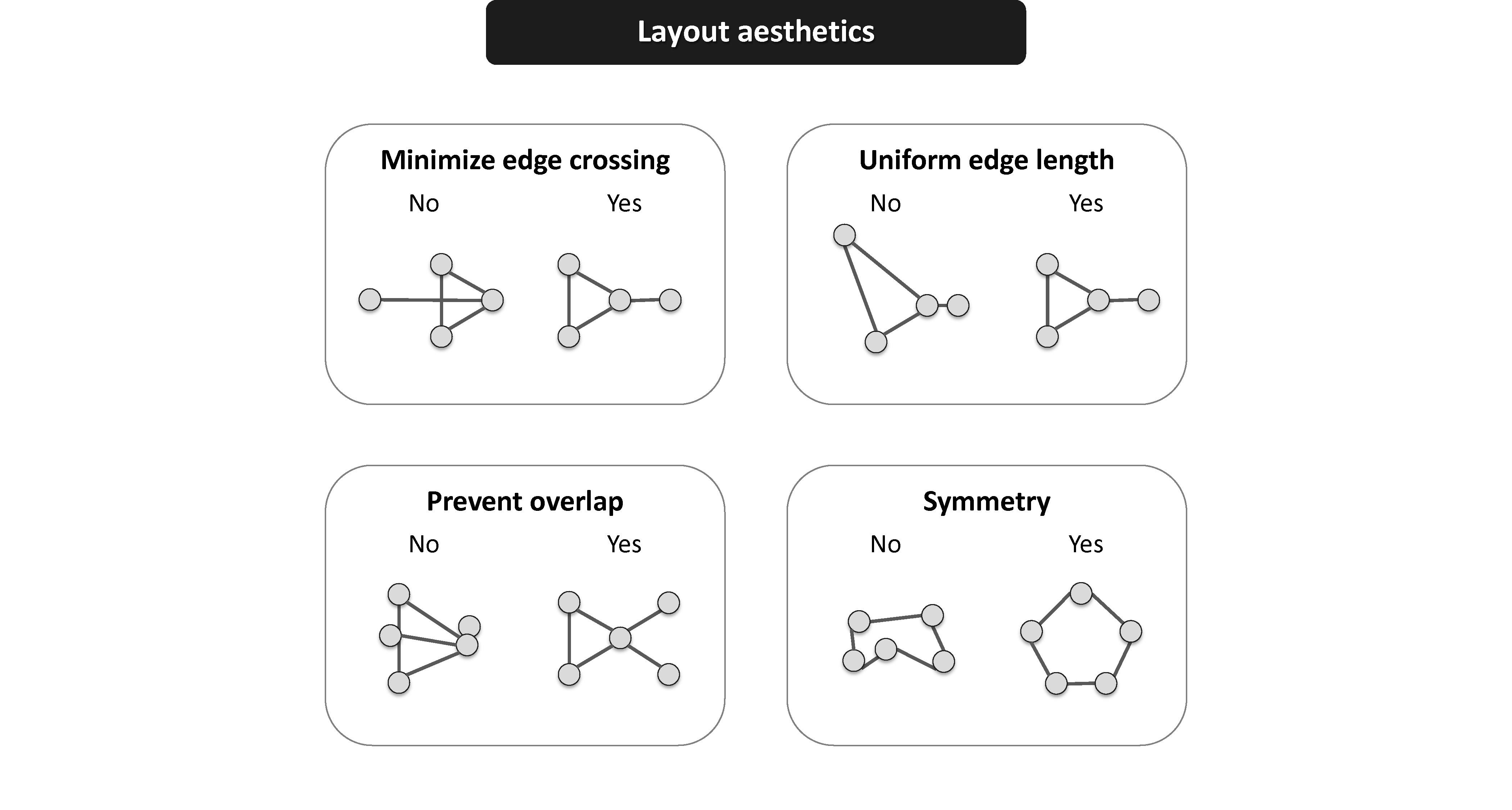
Для автоматического построения укладок разработано большое количество методов. В пакете igraph для каждого есть особая функция:

  • layout_randomly
  • layout_in_circle
  • layout_on_sphere
  • layout_with_drl (Distributed Recursive Layout)
  • layout_with_fr (Fruchterman-Reingold)
  • layout_with_kk (Kamada-Kawai)
  • layout_with_lgl (Large Graph Layout)
  • layout_as_tree (Reingold-Tilford)
  • layout_nicely

Можно выбрать укладку, не вызывая отдельную функцию:

ggraph(kfj_graph, layout = "kk") +
  geom_edge_link(alpha = 0.25) +
  geom_node_point(color = color, show.legend = F, size = 2) +
  geom_node_text(aes(label = names),  repel = TRUE) +
  theme_graph()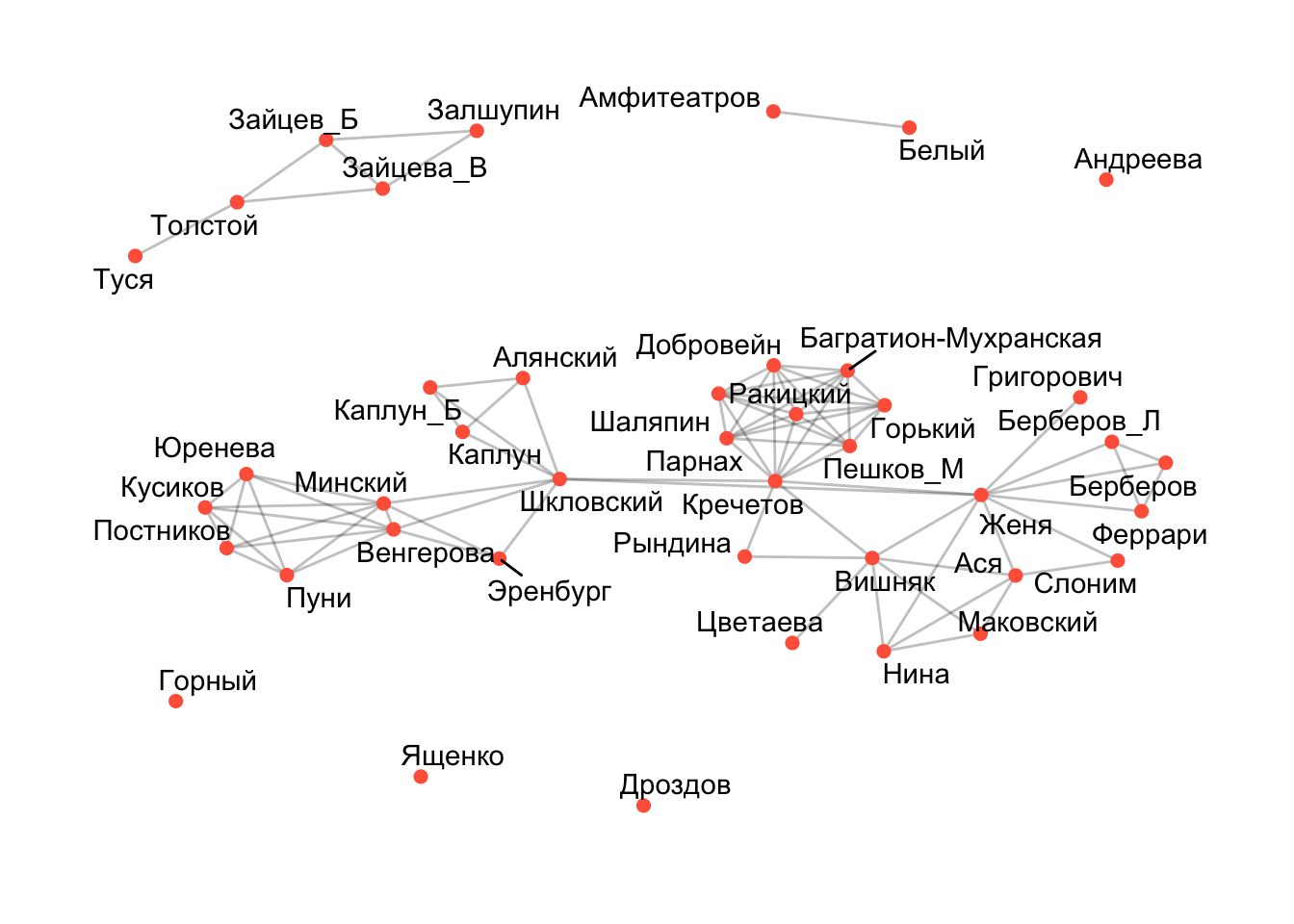

Поменяем укладку и цвета:

ggraph(kfj_graph, layout = "fr") +
  geom_edge_link(aes(color = "sienna"), 
                show.legend = F) +
  geom_node_point(size = 2, color = "olivedrab") +
  geom_node_text(aes(label = names),  repel = TRUE, color = "grey30") +
  theme_graph()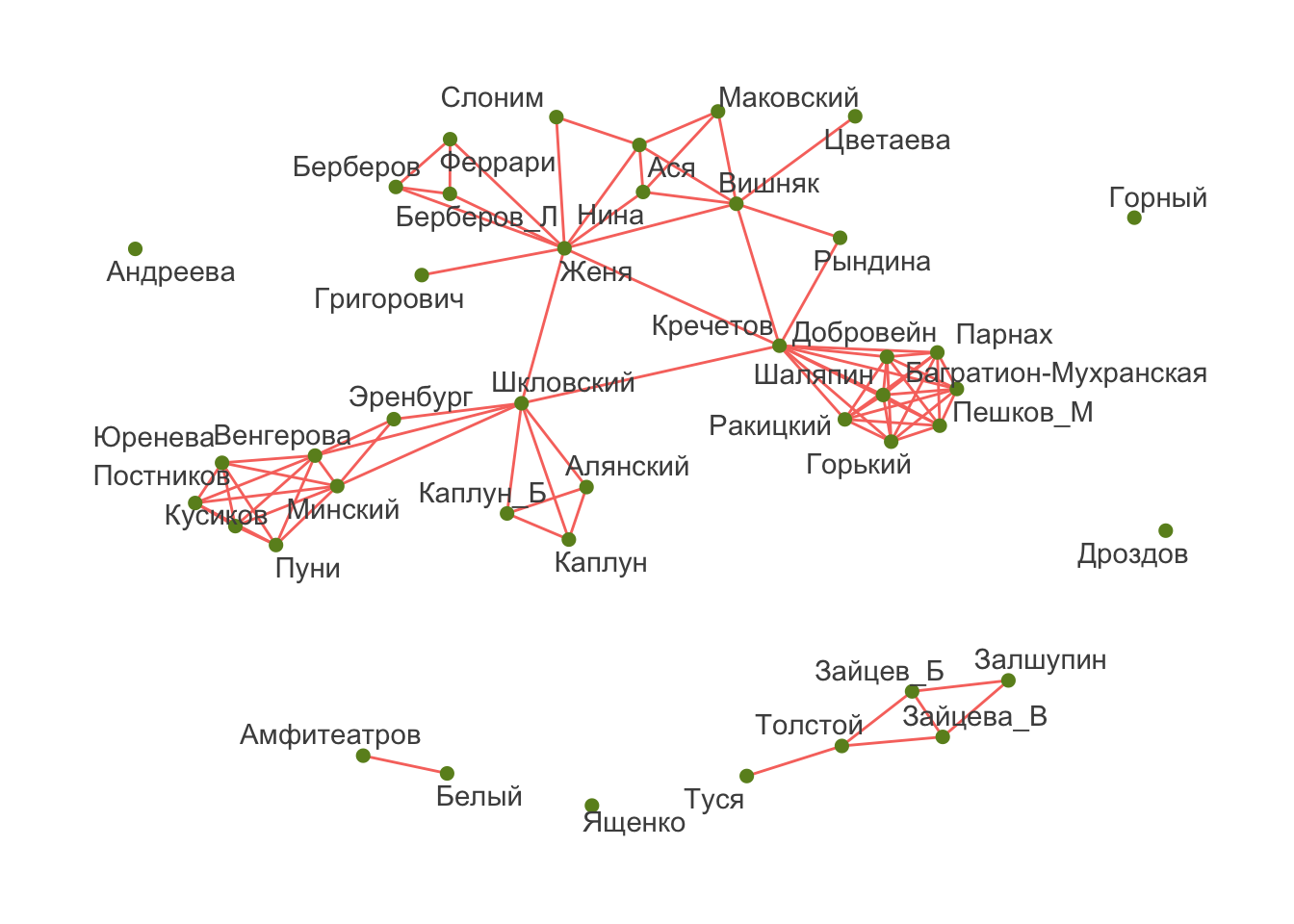

Не все укладки одинаково хороши.

ggraph(kfj_graph, layout = "linear", circular = T) +
  geom_edge_arc(aes(color = "sienna"), 
                show.legend = F) +
  geom_node_point(size = 2, color = "olivedrab") +
  geom_node_text(aes(label = names),  repel = TRUE, color = "grey30") +
  theme_graph()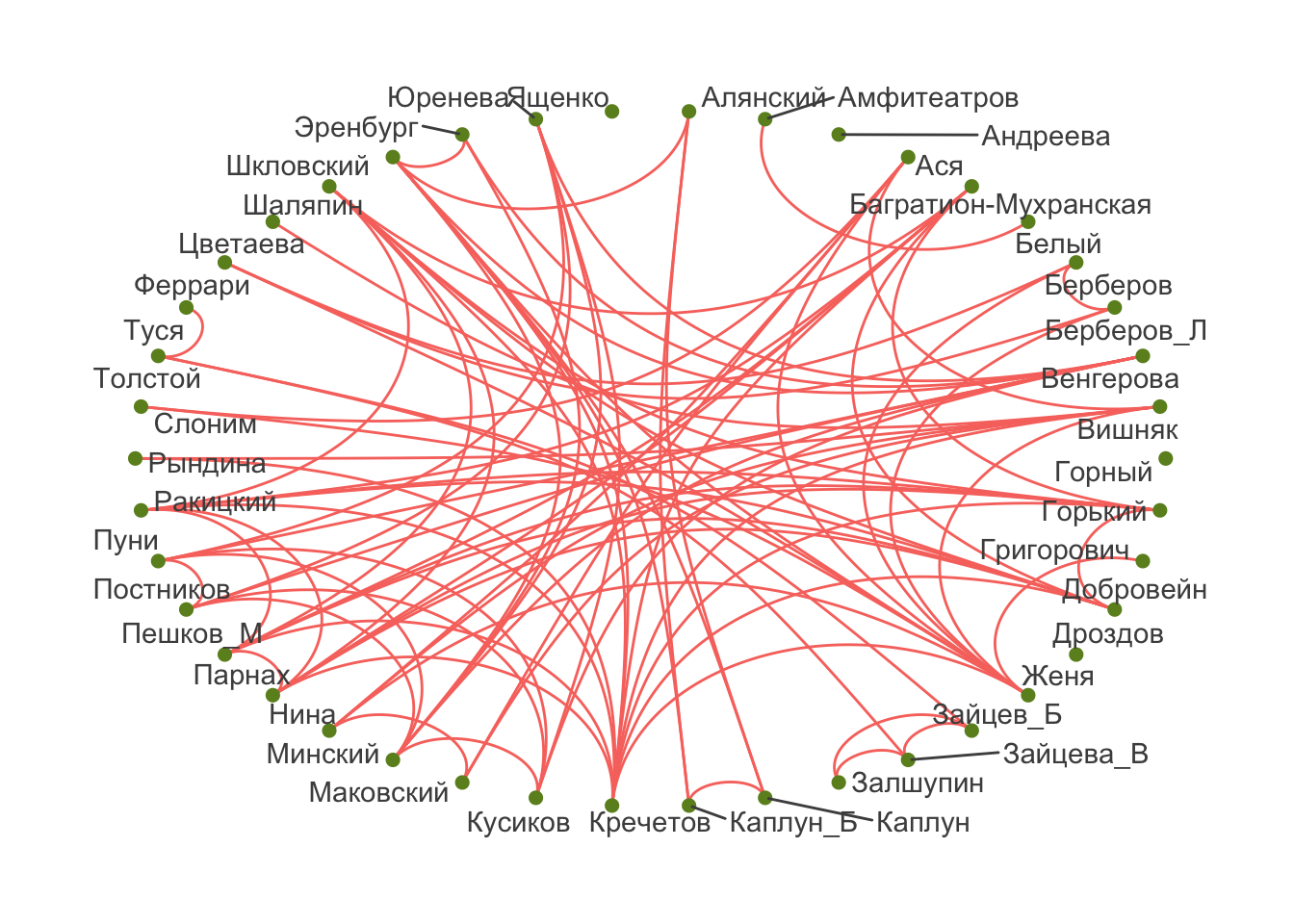

Подробнее см.: https://www.data-imaginist.com/2017/ggraph-introduction-edges/

Литература

Люк, Дуглас. 2017. Анализ сетей (графов) в среде R: Руководство пользователя. ДМК.

  1. https://habr.com/ru/articles/516514/↩︎

  2. https://kateto.net/netscix2016.html↩︎