Тема 17 Анализ сетей

Сети интересны своими паттернами взаимосвязей и тем, как эти паттерны влияют на участников сети.

Люк (2017)

В качестве участников сети можно рассматривать не только людей, но и, например, понятия. Пример подобного исследования см. в работе Б.В. Орехова “В сети терминов М. М. Бахтина: теория графов о диалоге, карнавале и хронотопе”. Узлами сети при таком моделировании становятся прежде всего важнейшие для системы автора термины, а сам граф отражает их взаимное функционирование в тексте. В частности, как показало это исследование, “кажущийся конструктивно важным элементом терминологической системы Бахтина хронотоп … на самом деле обладает минимумом связей (в терминах сетевого анализа число связей узла называется степенью) внутри графа”.

Мы попробуем провести похожее исследование, но за основу возьмем латинский текст “Исповеди” Августина.

17.1 От conllu к совместной встречаемости

Файлы “Исповеди” уже с размеченными частями речи, проверенный вручную, доступен в репозитории на GitHub. Эти файлы я заранее скачала в рабочую директорию курса.

files <- list.files("./files/augustinus/")
files

##  [1] "Augustinus_Confessiones_Liber1.tsv.conllu" 
##  [2] "Augustinus_Confessiones_Liber10.tsv.conllu"
##  [3] "Augustinus_Confessiones_Liber11.tsv.conllu"
##  [4] "Augustinus_Confessiones_Liber12.tsv.conllu"
##  [5] "Augustinus_Confessiones_Liber13.tsv.conllu"
##  [6] "Augustinus_Confessiones_Liber2.tsv.conllu" 
##  [7] "Augustinus_Confessiones_Liber3.tsv.conllu" 
##  [8] "Augustinus_Confessiones_Liber4.tsv.conllu" 
##  [9] "Augustinus_Confessiones_Liber5.tsv.conllu" 
## [10] "Augustinus_Confessiones_Liber6.tsv.conllu" 
## [11] "Augustinus_Confessiones_Liber7.tsv.conllu" 
## [12] "Augustinus_Confessiones_Liber8.tsv.conllu" 
## [13] "Augustinus_Confessiones_Liber9.tsv.conllu"

Сначала их нужно прочитать.

library(udpipe)
filenames <- paste0("./files/augustinus/", files)
head(filenames)

## [1] "./files/augustinus/Augustinus_Confessiones_Liber1.tsv.conllu" 
## [2] "./files/augustinus/Augustinus_Confessiones_Liber10.tsv.conllu"
## [3] "./files/augustinus/Augustinus_Confessiones_Liber11.tsv.conllu"
## [4] "./files/augustinus/Augustinus_Confessiones_Liber12.tsv.conllu"
## [5] "./files/augustinus/Augustinus_Confessiones_Liber13.tsv.conllu"
## [6] "./files/augustinus/Augustinus_Confessiones_Liber2.tsv.conllu"

library(tidyverse)
library(purrr)
confessions_ann <- map_df(filenames, udpipe_read_conllu)
confessions_ann <- confessions_ann %>% 
  select(-doc_id, -paragraph_id, -xpos, -feats, -head_token_id, -dep_rel, -deps, -misc)

head(confessions_ann)

##                        sentence_id
## 1 Augustinus_Confessiones_Liber1-1
## 2 Augustinus_Confessiones_Liber1-1
## 3 Augustinus_Confessiones_Liber1-1
## 4 Augustinus_Confessiones_Liber1-1
## 5 Augustinus_Confessiones_Liber1-1
## 6 Augustinus_Confessiones_Liber1-1
##                                     sentence token_id  token
## 1 magnus es , domine , et laudabilis valde .        1 magnus
## 2 magnus es , domine , et laudabilis valde .        2     es
## 3 magnus es , domine , et laudabilis valde .        3      ,
## 4 magnus es , domine , et laudabilis valde .        4 domine
## 5 magnus es , domine , et laudabilis valde .        5      ,
## 6 magnus es , domine , et laudabilis valde .        6     et
##     lemma  upos
## 1  magnus   ADJ
## 2     sum   AUX
## 3       , PUNCT
## 4 dominus  NOUN
## 5       , PUNCT
## 6      et CCONJ

Теперь можно посчитать совместную встречаемость, например, в рамках одного предложения. Для удобства визуализации я выберу только существительные, которые встречаются чаще 5 раз.

confessions_words <- confessions_ann %>%
  filter(upos == "NOUN") %>% 
  group_by(lemma) %>% 
  add_count() %>% 
  filter(n > 5) %>% 
  select(-n)

confessions_words

## # A tibble: 11,274 × 6
## # Groups:   lemma [431]
##    sentence_id                  sentence token_id token lemma upos 
##    <chr>                        <chr>    <chr>    <chr> <chr> <chr>
##  1 Augustinus_Confessiones_Lib… magnus … 4        domi… domi… NOUN 
##  2 Augustinus_Confessiones_Lib… magna v… 2        virt… uirt… NOUN 
##  3 Augustinus_Confessiones_Lib… magna v… 5        sapi… sapi… NOUN 
##  4 Augustinus_Confessiones_Lib… magna v… 9        nume… nume… NOUN 
##  5 Augustinus_Confessiones_Lib… et laud… 5        homo  homo  NOUN 
##  6 Augustinus_Confessiones_Lib… et laud… 9        crea… crea… NOUN 
##  7 Augustinus_Confessiones_Lib… et laud… 13       homo  homo  NOUN 
##  8 Augustinus_Confessiones_Lib… et laud… 19       test… test… NOUN 
##  9 Augustinus_Confessiones_Lib… et laud… 20       pecc… pecc… NOUN 
## 10 Augustinus_Confessiones_Lib… et laud… 23       test… test… NOUN 
## # ℹ 11,264 more rows

Теперь можно составить матрицу совместной встречаемости (и убрать редкие пары).

cooc <- cooccurrence(confessions_words, term = "lemma", group = "sentence_id")

cooc <- cooc %>% 
  as_tibble() %>% 
  filter(cooc > 10) %>% 
  rename(value = cooc)
cooc

## # A tibble: 264 × 3
##    term1      term2      value
##    <chr>      <chr>      <dbl>
##  1 caelum     terra        274
##  2 animus     memoria       55
##  3 dies       nox           48
##  4 caelum     principium    47
##  5 dominus    homo          45
##  6 spatium    tempus        44
##  7 nomen      terra         44
##  8 anima      corpus        43
##  9 imago      memoria       43
## 10 principium terra         43
## # ℹ 254 more rows

17.2 Граф слов с igraph

При создании графа уточним, что связи носят ненаправленный характер.

library(igraph)
confessions_graph <- graph_from_data_frame(cooc, directed = F)
confessions_graph

## IGRAPH 8b3a944 UN-- 102 264 -- 
## + attr: name (v/c), value (e/n)
## + edges from 8b3a944 (vertex names):
##  [1] caelum    --terra      animus    --memoria   
##  [3] dies      --nox        caelum    --principium
##  [5] dominus   --homo       spatium   --tempus    
##  [7] nomen     --terra      anima     --corpus    
##  [9] imago     --memoria    principium--terra     
## [11] caelum    --nomen      corpus    --sensus    
## [13] materia   --terra      homo      --uita      
## [15] abyssus   --terra      dominus   --deus      
## + ... omitted several edges

Попробуем изобразить (хотя для больших графов лучше строить интерактивную модель, в этом уроке наc больше интересует анализ связей, а не их визуализация).

library(ggraph)
ggraph(confessions_graph, layout = "fr") + 
  geom_edge_link(aes(edge_alpha = value)) +
  geom_node_point(color= "lightblue", size = 2) + 
  geom_node_text(aes(label = name, repel=T), vjust = 1, hjust = 1) + 
  theme_void()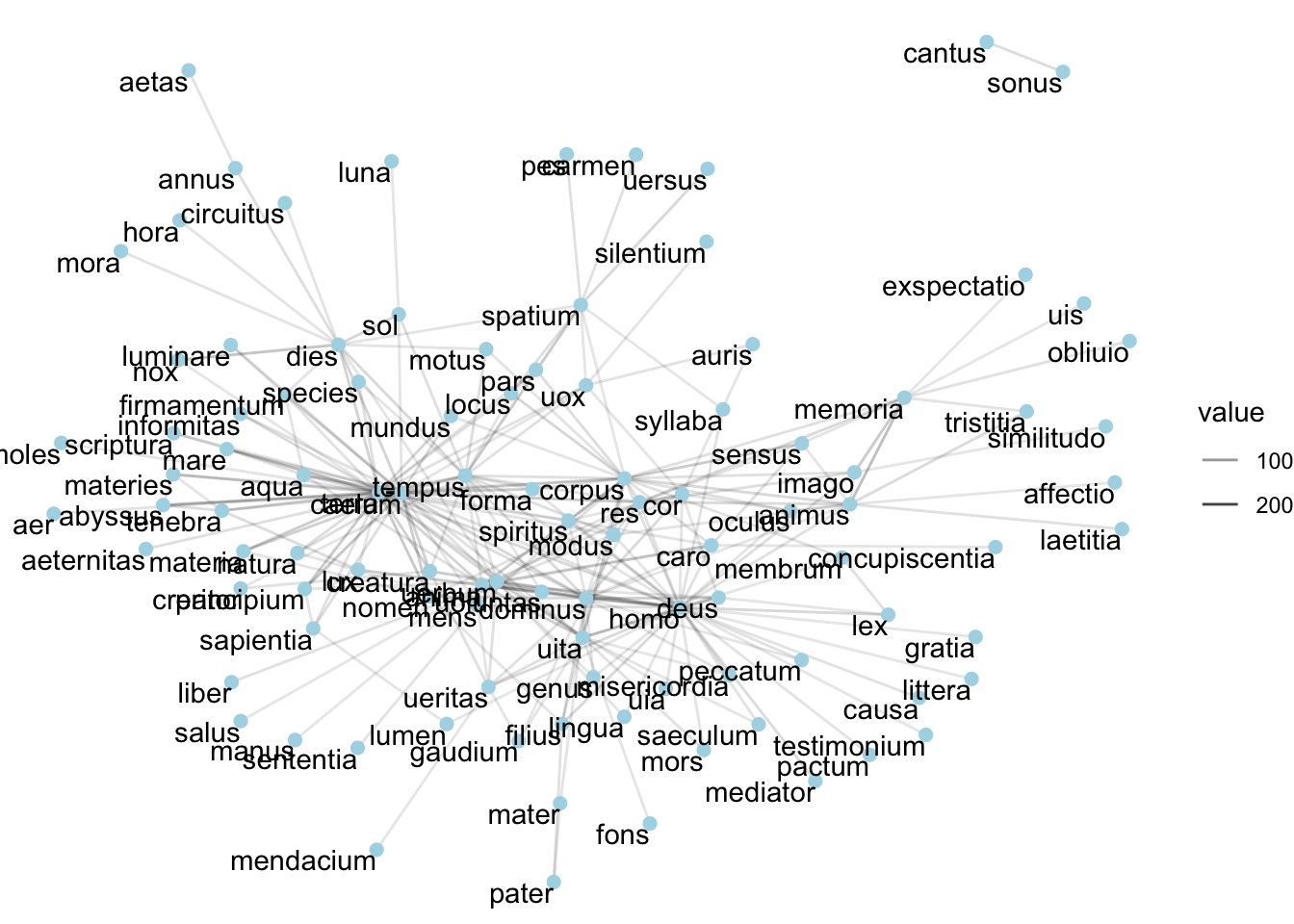

## Интерактивный график

Очень просто, но не очень смотрибельно.

# install.packages("networkD3")
library(networkD3)
simpleNetwork(cooc)

# conf_net <- simpleNetwork(cooc)
# saveNetwork(conf_net, file="Conf_net.html", selfcontained = T)

Можно чуть усложнить⁵⁷; код ниже, а результат смотрим здесь.

17.3 Важность узлов

Важность (prominence) участника (актора, вершины, узла) определяется его положением внутри сети. Применительно к ненаправленным сетям говорят о центральности (центральный актор вовлечен в наибольшее количество связей, прямых или косвенных), а применительно к направленным – о престиже. Престижный актор характеризуется большим количеством входящих связей.

Центральность по степени (degree centrality) определяется количеством связи: чем больше прямых связей, тем более важным является узел.

degrees <- degree(confessions_graph)
sort(degrees, decreasing = T)[1:10]

##    homo   terra  caelum  corpus dominus  tempus  uerbum   anima 
##      40      36      30      24      23      21      18      16 
##    uita     res 
##      16      14

Центральным понятием по степени для “Исповеди” является “человек”. Это слово имеет максимальное число связей.

Центральность по близости (closeness centrality) говорит о том, насколько близко узел расположен к другим узлам сети. Центральность по близости – это величина, обратная сумме расстояний от узла i до всех остальных узлов сети.

closeness <- closeness(confessions_graph)
sort(closeness, decreasing = T)[1:10]

##      cantus       sonus        homo       terra      caelum 
## 1.000000000 1.000000000 0.005813953 0.005649718 0.005434783 
##      corpus      tempus     dominus      uerbum         res 
## 0.005347594 0.005291005 0.005263158 0.005128205 0.004975124

Если обратиться к интерактивному графу, можно заметить, что cantus и sonus представляют собой отдельную компоненту. Собственно, только они туда и входят.

membership <- components(confessions_graph)$membership
table(membership)

## membership
##   1   2 
## 100   2

Поэтому уточним, что центральность по близости должна считаться для большей компоненты.

confessions_subgraph = induced_subgraph(confessions_graph, 
    which(membership == 1))
closeness <- closeness(confessions_subgraph)
sort(closeness, decreasing = T)[1:10]

##        homo       terra      caelum      corpus      tempus 
## 0.005813953 0.005649718 0.005434783 0.005347594 0.005291005 
##     dominus      uerbum         res       anima        uita 
## 0.005263158 0.005128205 0.004975124 0.004926108 0.004901961

И снова на первом месте “человек”.

Центральность по посредничеству (betweenness centrality) характеризует, насколько важную роль данный узел играет на пути “между” парами других узлов сети.

betweenness <- betweenness(confessions_graph)
sort(betweenness, decreasing = T)[1:10]

##      homo     terra    caelum    corpus      dies    tempus 
## 1476.0830 1055.3757  740.4504  619.8684  548.6346  515.2094 
##   dominus    uerbum   spatium   memoria 
##  439.5217  414.5475  325.8159  312.0012

Хороший пример персонажа с высокой степенью посредничества в корпусе русской драмы — второстепенный персонаж Гаврила Пушкин из пьесы «Борис Годунов» А.С. Пушкина. …По сюжету, он является связующим персонажем между приближёнными Бориса и Григорием. При прочтении легко не заметить важность этого персонажа, однако на визуализации сети пьесы хорошо видно, что Гаврила связывает два кластера — персонажей в Москве и в Польше.

Источник

Существуют и другие меры центральности, такие как центральность по собственному вектору, центральность по информации, и др.

17.4 Централизация

Централизация характеризует сеть в целом. Рассмотрим два крайних случая: круговой граф и звездчатый граф.

star_g <- graph.formula(a--b, a--c, a--d, a--e)
circle_g <- graph.formula(a--b, b--c, c--d, d--e, a--e)

par(mfrow = c(1, 2))
plot(circle_g, vertex.color=2)
plot(star_g, vertex.color=3)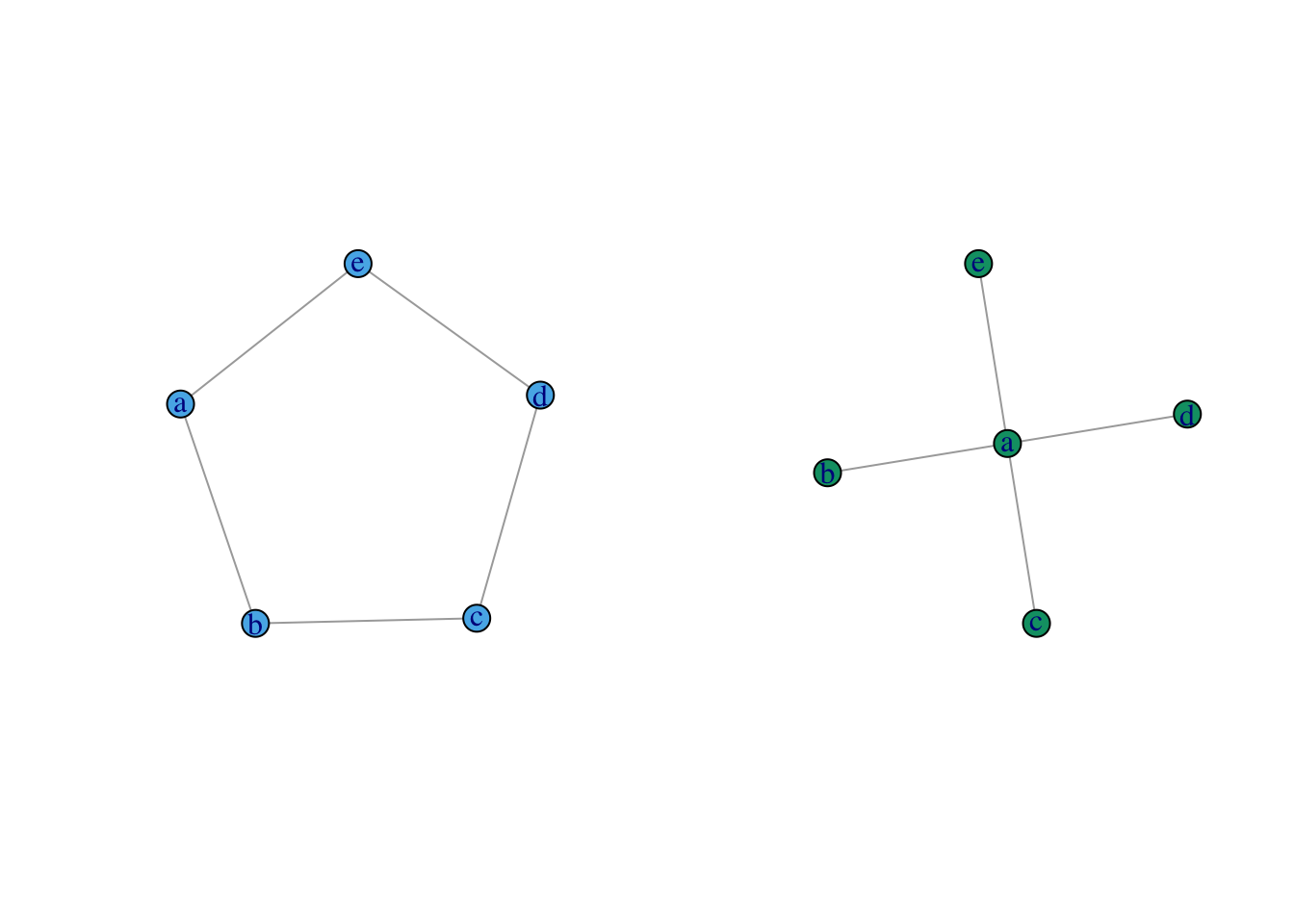

В случае звездчатого графа централизация максимальна, а для отдельных узлов наблюдается разброс центральности.

centralization.closeness(star_g)

## $res
## [1] 1.0000000 0.5714286 0.5714286 0.5714286 0.5714286
## 
## $centralization
## [1] 1
## 
## $theoretical_max
## [1] 1.714286

Во втором случае наборот – разброса нет, а для графа в целом централизация минимальна.

centralization.closeness(circle_g)

## $res
## [1] 0.6666667 0.6666667 0.6666667 0.6666667 0.6666667
## 
## $centralization
## [1] 0
## 
## $theoretical_max
## [1] 1.714286

Расчитаем централизацию для графа со словами из “Исповеди”.

names(centralization.closeness(confessions_graph))

## [1] "res"             "centralization"  "theoretical_max"

centralization.closeness(confessions_graph)$centralization

## [1] 1.240763

17.5 Центральность на графике

График сети, который включает в себя информацию о важности конкретных узлов, может быть эффективным инструментом анализа и визуализации. (Изменение формы на 21 нужно, чтобы можно было контур и заливку узла сделать разными цветами).

ggraph(confessions_graph, layout = "fr") + 
  geom_edge_link(aes(edge_alpha = value)) +
  geom_node_point(fill = "lightblue",
                  color= "grey30", 
                  size = log2(degrees) * 3, 
                  alpha = 0.5, 
                  shape = 21) + 
  geom_node_text(aes(label = name, repel=T), vjust = 1, hjust = 1) + 
  theme_void()

## Warning in geom_node_text(aes(label = name, repel = T), vjust = 1,
## hjust = 1): Ignoring unknown aesthetics: repel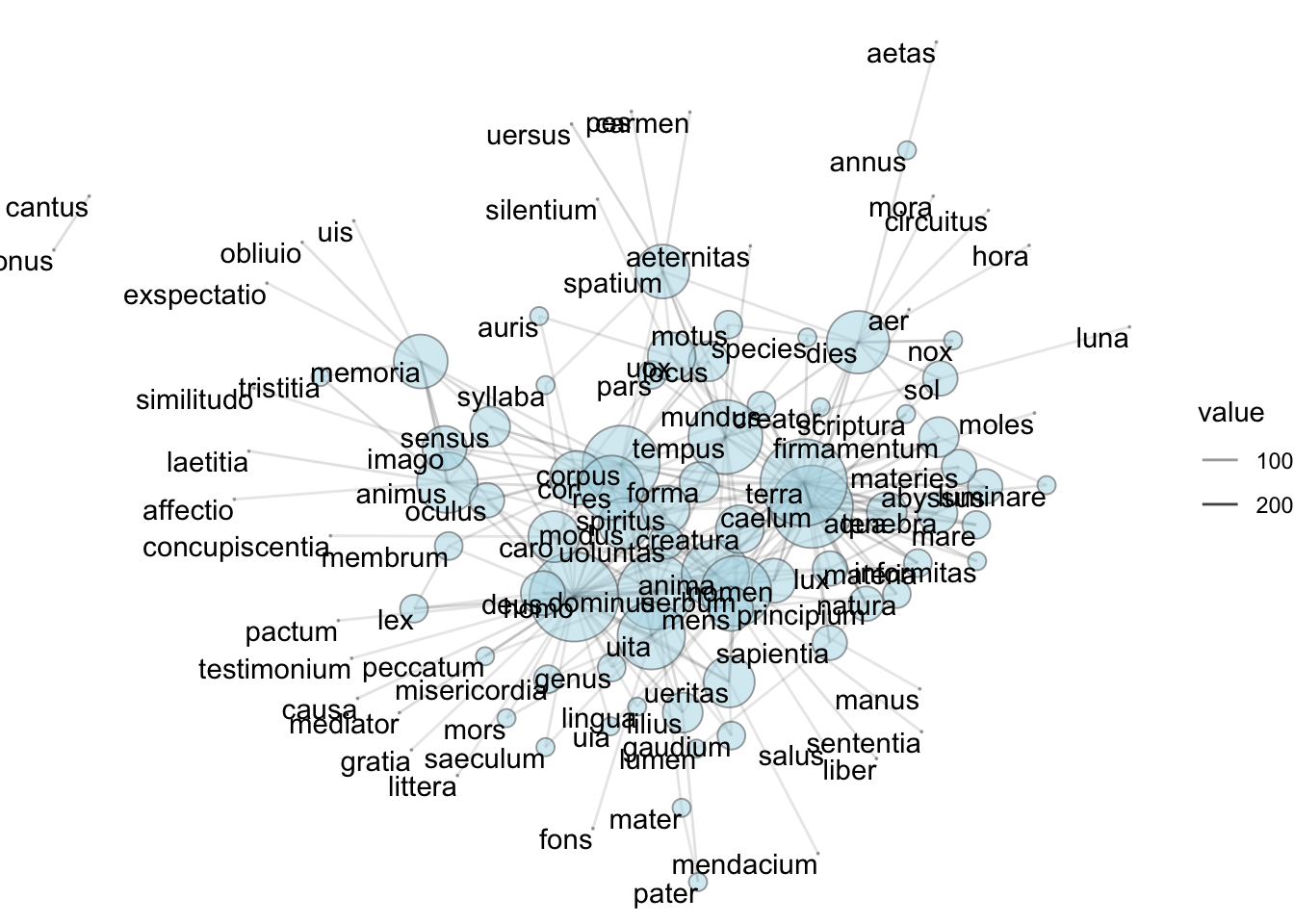

17.6 Интерактивный граф

Создадим интерактивный график (результат по ссылке выше).

#install.packages("visNetwork")
library(visNetwork)
data <- toVisNetworkData(confessions_graph)

# масштабированная центральность узла
data$nodes$value <- log(degrees)*3

confessions_3d <- visNetwork(nodes = data$nodes, 
                             edges = data$edges, 
                             width = "100%", 
                             height = 800)

Настраиваем и сохраняем график.

visOptions(confessions_3d, highlightNearest = list(enabled = T, degree = 1, hover = T), nodesIdSelection = T) %>%
  visPhysics(maxVelocity = 20, stabilization = F) %>% 
  visInteraction(dragNodes = T) %>% visSave(file = "Confessions.html")

17.7 Точки сочленения

Точка сочленения – это узел, при удалении которого увеличивается число компонент связности. Таким образом, они соединяют разные части сети. При их удалении акторы (узлы, вершины) не могут взаимодействовать друг с другом.

articulation_points(confessions_graph)

## + 16/102 vertices, named, from 8b3a944:
##  [1] uita    uox     caro    uerbum  ueritas tempus  sol    
##  [8] memoria imago   homo    anima   terra   animus  spatium
## [15] annus   dies

Например, oblivio и expectatio связаны с остальным графом только через “память”.

17.8 Подгруппы

Многие сети состоят из относительно плотных подгрупп, которые соединены между собой менее крепкими связями. Один из способов взглянуть на подгруппы сети заключается в исследовании социальной сплочености (cohesion). Сплоченные подгруппы - это множество акторов, которые объединены между собой посредством многочисленных, сильных и прямых связей.

17.8.1 Клики

Клика – один из самых простых типов сплоченных подгрупп; это максимально полный подграф, т.е. подмножество узлов со всеми возможными связями между ними.

Толковые словари понимают слово иначе. КЛИКА, -и; ж. [от франц. clique - шайка, банда] Неодобр. Группа, сообщество людей, стремящихся к достижению каких-л. корыстных, неблаговидных целей. Придворная к. К. финансовых дельцов. Фашистская к.

Вопреки своему названию, функция clique.number возвращает размер наибольшей клики:

clique.number(confessions_graph)

## [1] 7

cliques(confessions_graph, min=7)

## [[1]]
## + 7/102 vertices, named, from 8b3a944:
## [1] caelum  dominus homo    terra   tempus  res     uerbum 
## 
## [[2]]
## + 7/102 vertices, named, from 8b3a944:
## [1] caelum  dominus corpus  homo    terra   tempus  res

Или, что то же самое:

largest_cliques(confessions_graph)

## [[1]]
## + 7/102 vertices, named, from 8b3a944:
## [1] uerbum  homo    terra   tempus  res     dominus caelum 
## 
## [[2]]
## + 7/102 vertices, named, from 8b3a944:
## [1] res     corpus  tempus  terra   homo    dominus caelum

Но клика – это очень строгое определение сплоченной группы. Например, чтобы подграф, состоящий из 7 вершин, считался кликой, нужно, чтобы между ними было проведено \((7 \cdot 6) / 2 = 21\) связей. Если хотя бы одно ребро отсутствует, то условие не выполняется. Такие клики просто очень редко встречаются.

17.8.2 K-ядра

Популярным определением социальной сплоченности является k-ядро (k-core). Это максимальный подграф, в котором каждая вершина связана минимум с k другими вершинами этого же подграфа. K-ядра имеют множество преимуществ:

они вложены друг в друга (каждый участник 4-ядра является также участником 3-ядра и т.д.);
они не перекрываются;
их легко определить.

Выражение 6-ядро читают как “ядро степени 6”.

Ядро степени k+1 является подграфом ядра степени k. Любой узел в ядре степени k имеет степень либо k, либо выше. При этом coreness узла определяется по ядру с наибольшей степенью, к которому они принадлежат.

Для определения k-ядерной структуры используется функция graph.coreness():

coreness <- graph.coreness(confessions_graph)
head(coreness)

##  caelum  animus    dies dominus spatium   nomen 
##       7       5       4       7       4       4

Посчитаем количество вершин в ядрах.

table(coreness)

## coreness
##  1  2  3  4  5  6  7 
## 34 17 14 14 10  2 11

1-ядро содержит 34 вершины, 2-ядро содержит 17 вершин, и т.д.

Для лучшей интерпретации k-ядерной структуры мы можем графически изобразить сеть, используя информацию о множестве k-ядер. Для начала добавим информацию о цвете к атрибутам узлов. Сейчас, как можно убедиться, в списке атрибутов хранятся только имена:

names(get.vertex.attribute(confessions_graph))

## [1] "name"

V(confessions_graph)$color <- coreness
names(get.vertex.attribute(confessions_graph))

## [1] "name"  "color"

ggraph(confessions_graph, layout = "fr") + 
  geom_edge_link(edge_alpha = 0.2) +
  geom_node_point(aes(fill = as.factor(color)),
                  color= "grey30", 
                  size = log2(degrees) * 4, 
                  alpha = 0.5, 
                  shape = 21) + 
  geom_node_text(aes(label = name), vjust = 1, hjust = 1) + 
  theme_void()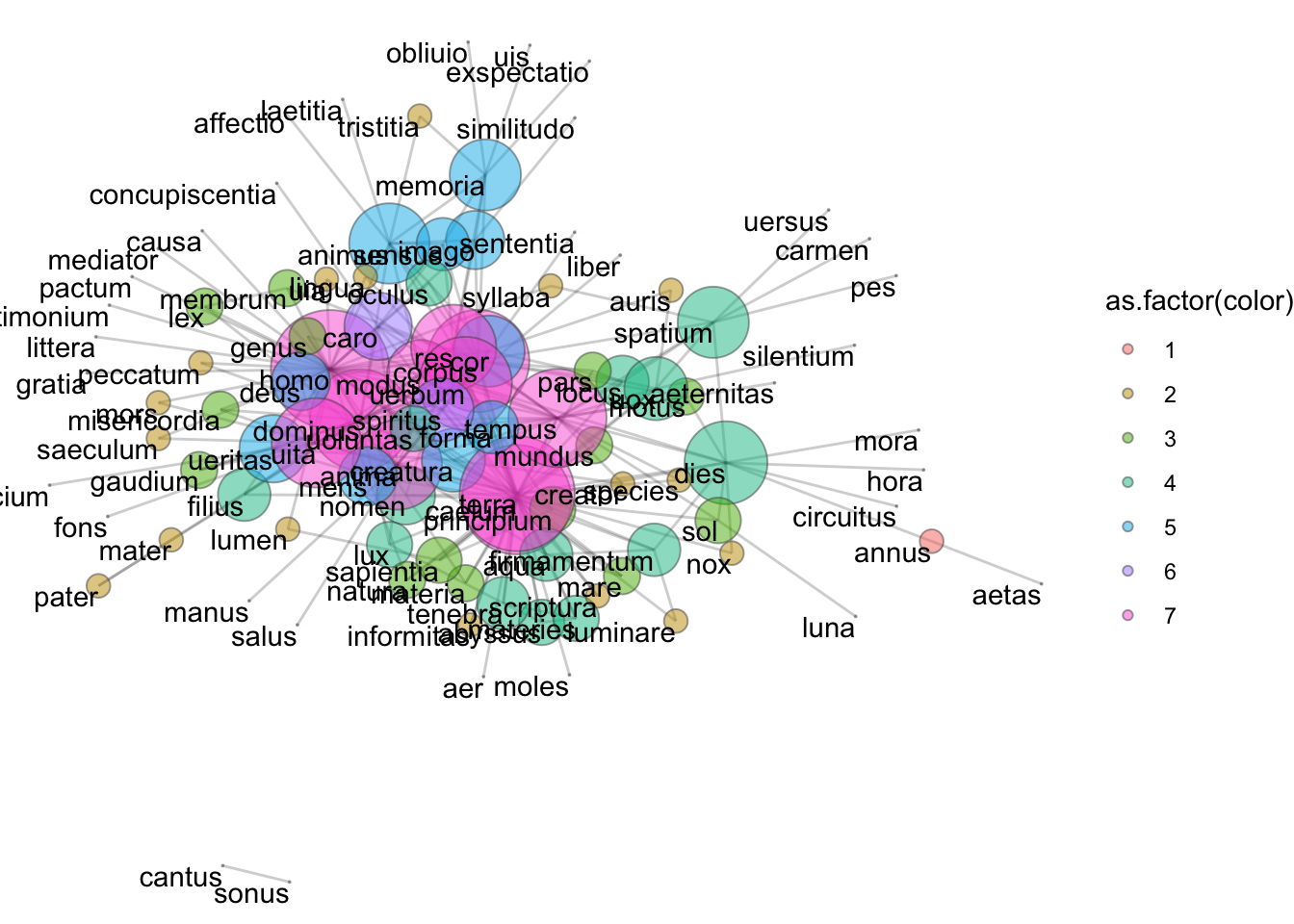

Сейчас граф не очень читается, но видно, что в центре находятся ядра наивысшей степени. В данном случае речь идет о 7-ядре, которому принадлежит 11 узлов. Т.е. из этих 11 узлов каждое связано не менее чем с 7 другими участниками группы.

Чтобы глубже исследовать подгруппы, последовательно удаляют k-ядра более низкой степени. Для этого можно воспользоваться функцией induced_subgraph().

confessions3_7 <- induced_subgraph(confessions_graph, vids=which(coreness > 2))

ggraph(confessions3_7, layout = "fr") + 
  geom_edge_link(edge_alpha = 0.2) +
  geom_node_point(aes(fill = as.factor(color)),
                  color= "grey30", 
                  size = 4,
                  alpha = 0.5, 
                  shape = 21) + 
  geom_node_text(aes(label = name), vjust = 1, hjust = 1) + 
  theme_void()

При интерпретации важно помнить, что ядра являются вложенными. Чем выше степень ядра, тем больше узлы связаны между собой.

confessions6_7 <- induced_subgraph(confessions_graph, vids=which(coreness > 5))

ggraph(confessions6_7, layout = "fr") + 
  geom_edge_link(edge_alpha = 0.2) +
  geom_node_point(aes(fill = as.factor(color)),
                  color= "grey30", 
                  size = 4,
                  alpha = 0.5, 
                  shape = 21) + 
  geom_node_text(aes(label = name), vjust = 1, hjust = 1) + 
  theme_void()

Литература

Люк, Дуглас. 2017. Анализ сетей (графов) в среде R: Руководство пользователя. ДМК.

https://datastorm-open.github.io/visNetwork/physic.html ↩︎